Impedance Matching with Parallel Tx Line Stubs
|
On the previous page we introduced
impedance matching with parallel inductors and capacitors.
On this page, we'll illustrate how transmission lines can be placed in parallel to
perform impedance matching.
Short-Circuited Tx LinesIf you haven't already, you will need to review the short and open circuited transmission lines page. From that page, the impedance and admittance of a short circuited tx line is shown to be:
 [1] [1]Using a transmission line instead of a lumped inductor can be advantageous, because tx lines tend to have lower loss than lumped inductors, particularly for larger inductance values. The disadvantage is they can take up more space, creating a larger physical impedance matching network. Also, their out of band perfomrance is different from lumped elements, and all of these factors needs taken into account to choose the right matching component.
Open Circuited Tx LinesThe impedance and admittance of an open-circuited tx line is:
 [2] [2]Equation [2] states that we can use an open-circuited line (with a length less than a quarter-wavelength) to create a capacitive impedance. That is, the tx line will have Re[Zin]=0 and Im[Zin]<0 for 0 < L < lambda/4.
Impedance Matching with Parallel (Shunt) Transmission Lines
We'll now perform impedance matching with only transmission lines. This method
will work for any impedance on the Smith Chart for which the magnitude of
Consider the load admittance yL = 0.3 + i*0.5 (then zL = 0.882 - i*1.471).
The absolute value of
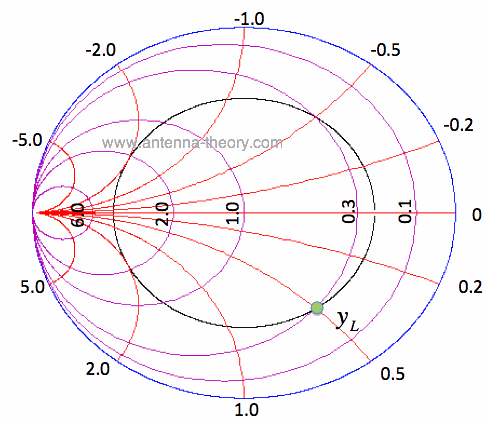 Figure 1. Load Admittance and the Corresponding Constant SWR Circle. To match the load of Figure 1 with a parallel (shunt) component, we will need to swing the load admittance around on the Smith Chart until it intersect the Re[y]=1 constant conductance circle. That is, if we add a length of transmission line in front of the load admittance, we can move the load yL along the black constant SWR circle of Figure 1 until it intersects the Re[y]=1 circle. Then a parallel transmission line section can be used to cancel out the susceptance (the imaginary part of the admittance), such that the load will be exactly matched.
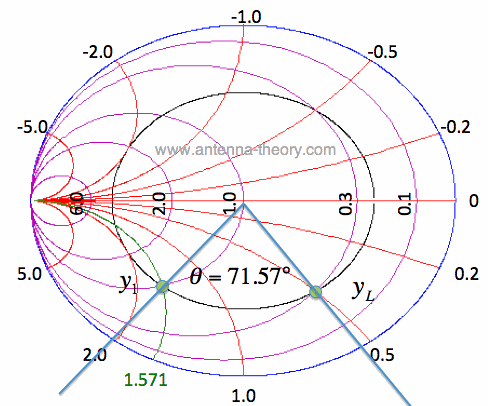 Figure 2. Determining Transmission Line Length to Intersect the Re[y]=1 Circle. Using equation [1] on the impedance matching with tx lines page, we can calculate that the angle 71.57 degrees corresponds to a line length of roughly 0.0994 wavelengths. From the point y1 shown in Figure 2, we bring the admittance to the center of the Smith Chart with a parallel inductance, of y_sc = -i*1.571. On this page, we will implement this with a short-circuited shunt tx line. Using equation [1] from above, we can get the line length:
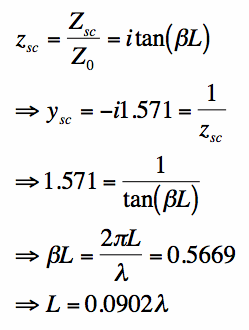 [3] [3]Hence, we can use a shorted transmission line of length L=0.0902 wavelengths to create an inductance that cancels the susceptance of y1. This impedance matching network is shown in Figure 3.
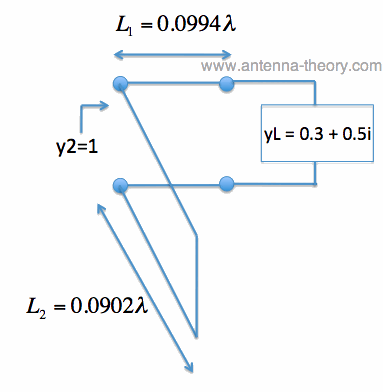 Figure 3. Impedance Matching Network Using only Tx Lines. The final impedance, y2, is equal to 1 as shown in Figure 3. The path taken by load yL, using the matching transmission lines, is shown on the Smith Chart in Figure 4.
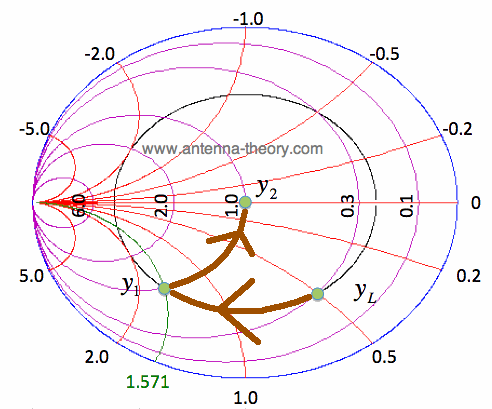 Figure 4. The Impedance Matching Path Corresponding to the Network of Figure 3. The key to understanding this section is realizing that a parallel susceptance can be used to match any load/admittance/impedance that intersects the Re[y]=1 constant conductance circle. In the next section, we'll look at matching without tx lines.
Smith Chart (Home) Topics Related To Antenna Theory
|
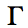 is less than 1. This method is very similar to the techinique given on the
is less than 1. This method is very similar to the techinique given on the