Transmission Lines: Open and Short Circuit Lines

Short-Circuited Lines

Consider a transmission line of length L, but suppose the end of the line is short-circuited together (so that ZA=0). Then from the impedance equation:

We can determine the input impedance (or input admittance = 1/Z) for a short circuited line:

      [1]

The above equation states that by using a short circuited transmission line, we can add a reactive impedance to a circuit. This can be used for impedance matching, as we'll illustrate.

Example. Suppose an antenna has an impedance of ZA = 50 - j*10. Using a short-circuited transmission line (with Z0=50 and u=c) in parallel with the antenna, transform the input impedance to be entirely real (zero reactance).

Solution. The problem is illustrated below.

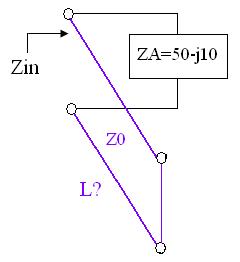We are trying to use a short-circuited transmission line to make the input impedance purely real (cancel out the capacitive reactance of the load). [Also note that we could further transform the real impedance by using a quarter-wave transformer at the terminals above.]

The admittance of the load is:

If a reactance is added in parallel with a value of YA = -j*0.0038, the admittance will be entirely real, so the impedance will also be entirely real. Using equation [1], we can solve for the length of the transmission line so that YA = -j*0.0038:

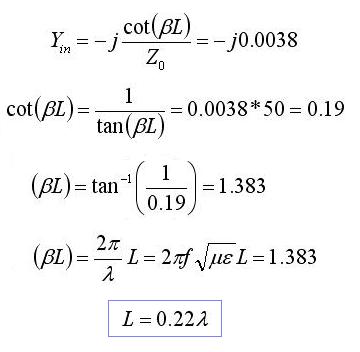Hence, if a short-circuited transmission line of length 0.22 wavelengths is added in parallel with the load, then the admittance will be entirely real and given by Yin=0.0192. Hence, the input impedance Zin = 1/Yin = 52 Ohms.

Open-Circuited Transmission Lines

Note that we can use open- and short-circuited transmission lines as substitutes for inductors and capacitors if a reactance is desired. This is often done in practice.

How would you go about measuring the characteristic impedance of a transmission line? There is a simple solution. If you measure the open- and short-circuited impedances of a transmission line for any fixed length L, the characteristic impedance (Z0) can be determined:

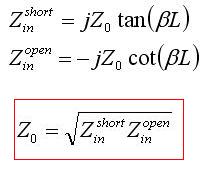The square root of the product of the measurements gives the characteristic impedance of the line. This method is easy and commonly done in practice.

This concludes the transmission line tutorial.