Smith Chart Tutorial - Impedance Matching with Tx Lines, Series L and C
|
On the previous page, we showed
how to use series inductors and capacitors to cancel out the reactance of a load. However, as seen
in the
second example on the previous page,
this method won't work unless the real part of the load impedance is 1 (that is, Re[ZL]=1). On this page,
we'll show how to use transmission line sections and a series component to exactly match any load impedance. Let's look at example 2 from the previous page again. That is, let zL = 0.3 + i. Instead of using a component, suppose we use a transmission line section to move the impedance. We know from the page on impedance transformations that a transmission line section will enable the load impedance to move in a circle about the center of the Smith Chart. That is, given the load impedance zL, a transmission line section can relocate the impedance to any location in the black circular ring of Figure 1:
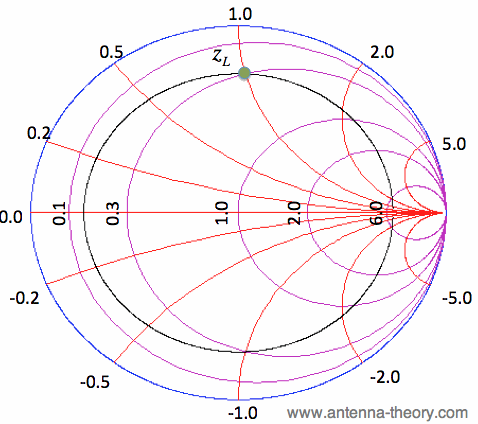 Figure 1. Impedance zL on the Smith Chart along with its constant VSWR circle. Recall that if an impedance is of the form z1 = 1 + iX, then we can exactly match it using a series inductor or capacitor. Now, if we use a transmission line section to rotate the impedance on the Smith Chart until it intersects the Re[z]=1 circle, then we can exactly match any impedance that does not have a reflection coefficient magnitude equal to 1 (that is, we can match anything on the interior of the Smith Chart). To figure out the rotation needed, draw a line from the center of the Smith Chart through zL, and then draw another line from the center of the Smith Chart to the location where the constant SWR circle intersects the Re[Z]=1 circle. Then find the angle between the two lines, as shown in Figure 2.
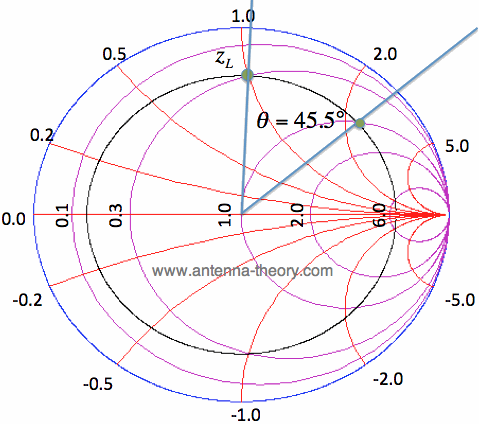 Figure 2. Determining the Tx Line Length to Reach the Re[Z]=1 circle. In Figure 2, we have found the angle between the two lines to be 45.5 degrees. This can be done in different ways; for example, by drawing the lines and then using a protracter to determine the angles, or reading off the angle difference using the degrees scale on the outer rim of the smith chart. Since one wavelength corresponds to two complete rotations around the Smith Chart, we have:
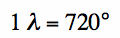 [1] [1]We can calculate the required length of the transmission line corresponding to 45.5 degrees:
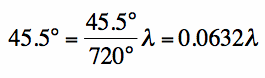 [2] [2]
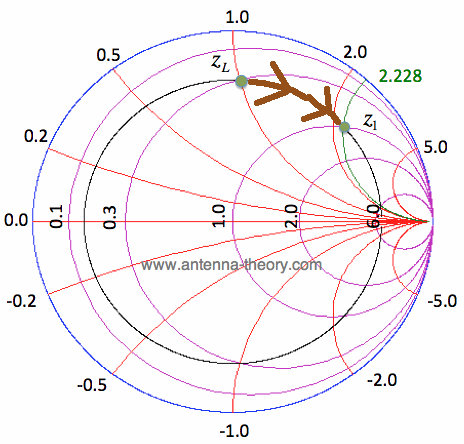 Figure 3. Effect of Tx line (length = 0.0632 wavelengths) on zL. In Figure 3, I've also drawn in green the constant reactance curve given by Im[Z]=2.228. This is exactly where the constant VSWR circle intersects the Re[z]=1 constant resistance circle. The resultant impedance is z1 (shown in Figure 3), and the value for this can be read directly off the smith chart yielding z1 = 1 + i*2.228. For clarity, note that z1 is the impedance shown in Figure 4:
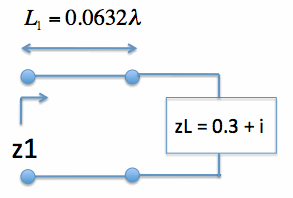 Figure 4. Illustration of Tx Line and load zL. Since z1 = 1 + i*2.228, we can exactly match this impedance to the center of the Smith Chart uses a series capacitor. We simply choose C such that z_cap = -i*2.228, and the impedance z2 will be 1.0. For details on how this is done, see previous page. The path taken by zL to reach the center of the Smith Chart is shown via the brown curve in Figure 5. 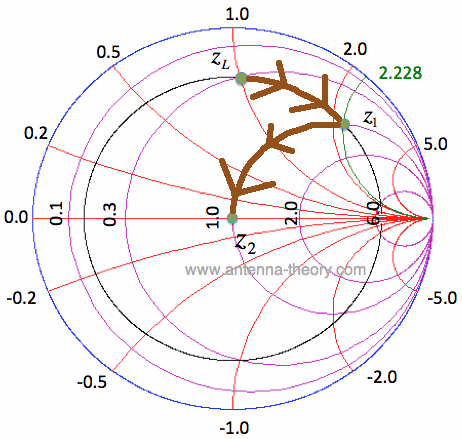 Figure 5. Moving zL to z1 and then z2 with a tx line and series capacitor. The resulting impedance matching network is shown in Figure 6. The result is that z2 = 1, so that no power is reflected at z2:
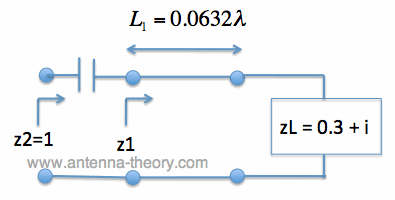 Figure 6. Impedance zL exactly matched (z2=1).
RecapThe above technique can be used for any impedance on the interior of the Smith Chart. The result will be zero reflection at the matching network. To sum up the procedure:
The problem with the above method is that it works for a single band (not ok if you want dual band matching) and it requires a tx line which can take up too much space. We'll look at other methods, involving parallel components in the coming sections.
Smith Chart (Table of Contents) Topics Related To Antenna Theory Antennas (Home)
|