The Admittance Smith Chart
|
The discussion thus far has centered around the "standard" Smith Chart, also known as the impedance Smith Chart. The impedance Smith Chart isn't great for working with parallel components (parallel inductors, capacitors or shunt transmission lines).
To generalize the Smith Chart and to make things easier for parallel impedance matching, we will now introduce the Admittance Smith Chart.
Admittance Smith Chart
Recall that on the standard or impedance Smith Chart, the circles and curves related to constant resistance and constant reactance. That is, we are looking at the impedance of an antenna, or load (Z_L). Impedances are great for dealing with series components - the impedances simply add. However, for parallel components the math becomes tricker. To simplify this, we can simply look at the admittance of an antenna (or load, Y_L). The admittance will be written as:
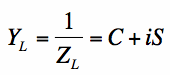 [1] [1]
In equation [1], Y_L is the admittance of the load, which is the inverse of the impedance of the load (Z_L). The real part of Y_L is written as C, and is known as the conductance. The imaginary part of Y_L is written as S, and is known as the susceptance.
Note that the admittance Smith Chart will still plot the reflection coefficient
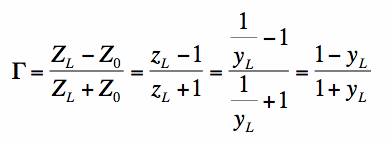 [2] [2]
We will again be dealing with normalized admittances (y_L), which will be related to the normalized impedance z_L by:
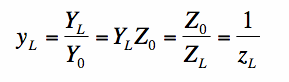 [3] [3]In equation [3], Y_0 is equal to 1/Z_0.
Constant Conductance Circles
We know that we can take any admittance, y, and plot it on the Smith Chart, since y=1/z. Suppose we would like to know where the constant conductance circles are. For example, what curve makes up Re[y] = 1? That is, if y1 = 1 + i*G, where G is any real number, what is the curve defined by y1? We can numerically evaluate this using equation [2], and the result is shown in Figure 1:
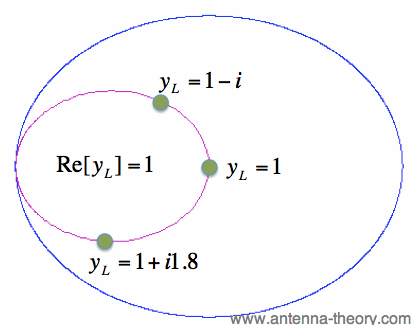 Figure 1. Constant Conductance Circle for Re[y]=1.
A few examples for y_L values are plotted along the constant conductance circle shown in Figure 1. Again, the outer blue circle in Figure 1 represents the boundary of the Smith Chart; this is where the magnitude of the reflection coefficient is unity.
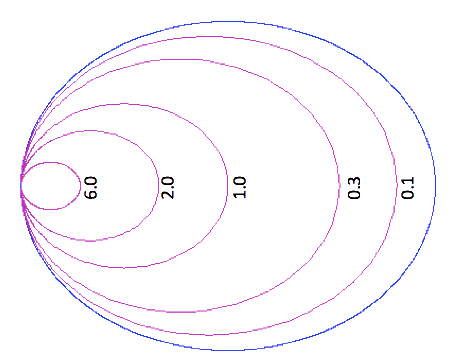 Figure 2. Constant Conductance Circles on Admittance Smith Chart.
The smallest circle on the left in Figure 2 is the Re[y]=6 circle. The largest purple circle is Re[y]=0.1. Several other constant conductance circles are shown in Figure 2. These will be very useful for impedance matching with parallel components.
Constant Susceptance Curves
Suppose we are interested in where the constant susceptance curves are. That is, where is the curve given by y_L = A + i, where A is a positive real number? Using a bunch of math, or just methodically plotting points using equation [2], we can obtain the red curve in Figure 3:
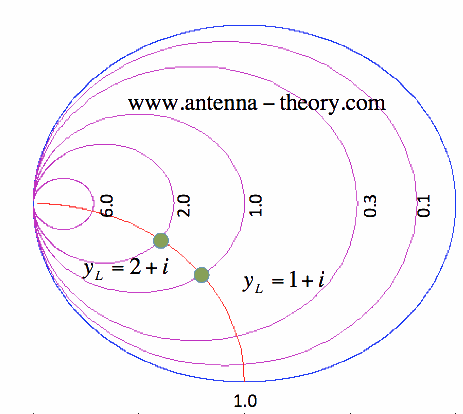 Figure 3. Constant Susceptance Curve for Im[yL]=1.
Note that positive values of susceptance lie on the southern hemisphere of the Smith Chart, whereas positive values of reactance lie on the northern hemisphere of the Smith Chart. To complete the admittance Smith Chart, we will sketch several more constant susceptance curves, as shown in Figure 4:
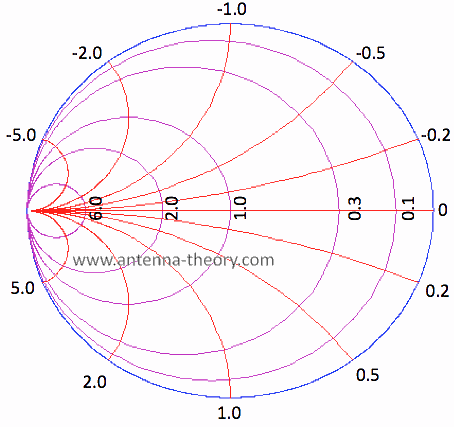 Figure 4. Constant Susceptance Curves on Admittance Smith Chart. On the next page, we'll introduce the immitance Smith Chart, and look at parallel components for impedance matching.
Previous: Impedance Matching with Series L, C and Tx Lines Smith Charts (Main) Topics Related To Antenna Theory
|
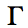 exactly as before. The admittance Y can be related back to the reflection coefficient by
rewritting
exactly as before. The admittance Y can be related back to the reflection coefficient by
rewritting