Immittance Smith Chart - Matching without Tx Lines

On this page, we'll look at impedance matching with both series and parallel components. It turns out, that if we combine the impedance Smith Chart with the admittance Smith Chart, we will have no trouble doing this. The combination is known as the Immittance Smith Chart.

Immittance Smith Chart

If we overlay the impedance Smith Chart on top of the admittance Smith Chart, we get the Immittance Smith Chart of Figure 1:

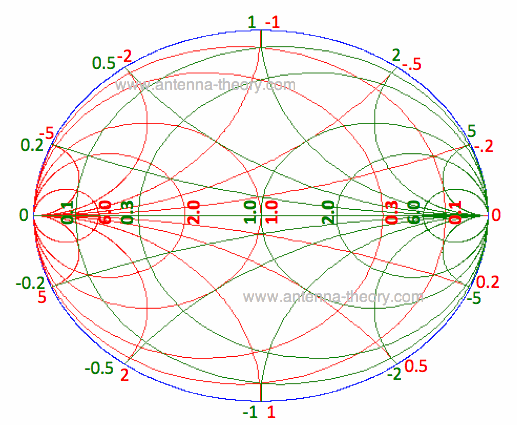Figure 1. The Immittance Smith Chart.

The immittance Smith Chart of Figure 1 looks insanely complicated. But it is just the admittance Smith Chart in red overlayed on top of the impedance Smith Chart in green. This Smith Chart, while it looks like chaos, is extraordinarily helpful.

The reason Figure 1 is awesome: whether we want to know how a parallel component or a series component affects the impedance, we can visualize it using the immittance chart. Parallel capacitors, inductors and transmission lines will affect the load impedance by movement along the constant conductance circles (in red). Series capacitors and inductors affect the load or antenna impedance by translation along the constant resistance circles (in green). Finally, even though we haven't talked about it and it isn't used much for impedance matching with antennas, series resistors will move an impedance along the constant reactance curves, and parallel resistors will move an impedance along the constant susceptance curves.

Using the Immittance Smith Chart, we can match any impedance (with a reflection coefficient magnitude less than 1) using a capacitor and an inductor. Here's a fundamental observation:

If an impedance intersects the Re[z]=1 constant resistance circle, then it can be matched with a series inductor or capacitor. If an impedance intersects the Re[y]=1 constant admittance circle, then it can be matched with a parallel inductor or capacitor. Hence, we will use a single component to move the impedance on the Immittance Smith Chart such that it intersects the Re[z]=1 circle or the Re[y]=1 circle, and then use the second component to move it to the center of the Smith Chart.

Example 1

Suppose an antenna has an impedance of z_A=0.1-i0.2. We know that a series inductor will move this impedance in a clockwise direction along the Re[z]=0.1 circle. We would like to move this impedance along this circle until it intersects the Re[y]=1 circle.

Using the immittance Smith Chart of Figure 1, we will need to move the antenna admittance

(y_A = 1/z_A = 2 + 4i ) along the Re[z]=0.1 circle, as shown in Figure 2:

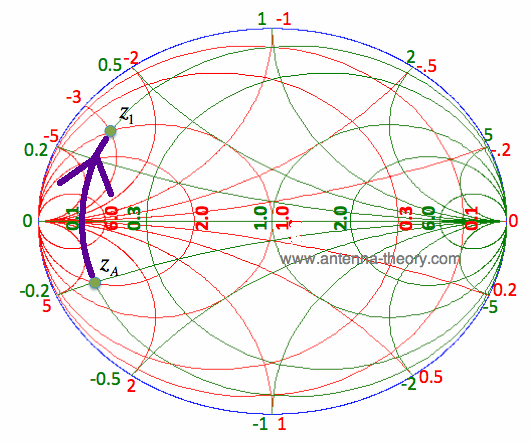Figure 2. Moving the Antenna Impedance with a Series Inductance.

If an inductor with a normalized reactance z_L = i0.5 is added in series to z_A (see eq [1] inductor reactance), the result is

z_1=0.1 +i0.3 shown in Figure 2. Note that

y_1 is equal to 1 - 3i, which places us on the Re[y]=1 circle, which is where we want to be.

Now we can use a parallel component to move the impedance z_1 to the center of the Smith Chart. Since y_1 = 1 - 3i, we can use a capacitor with a normalized susceptance of 3 (recall from admittance charts page that the susceptance is the imaginary part of the admittance, and this is positive for a capacitor, see equation [3] on the parallel L and C page). The exact value for the capacitance depends on what frequency we are interested in. The parallel capacitor moves the impedance z_1 along the constant conductance circle as shown in Figure 3:

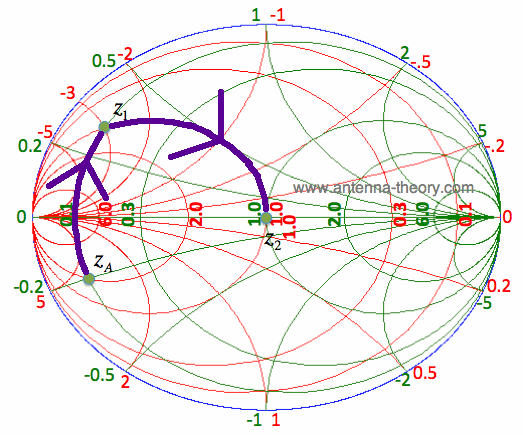Figure 3. Completing the Impedance Matching.

Hence, we have matched the impedance z_A with a series inductor and a parallel capacitor. This matching network is shown in Figure 4.

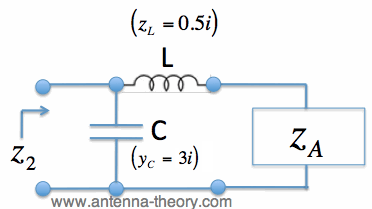Figure 4. Impedance Matching Network for Example 1.

On the next page, we'll look at different impedance matching networks that accomplish the same goal.