Capacitance
| Electric Charge | Electric Field | Magnetic Field | Antennas (Home) |
| Lenz's Law | Inductance | Capacitance | E-Field Conditions |
| H-Field Conditions |
|
So if Inductance is associated with stored energy in the magnetic field, what represents stored energy in the Electric Field? This is the topic of Capacitance. Consider a sinusoidal voltage applied across two conductive parallel plates, separated by a distance d. A sinusoidal voltage is simply a time-varying voltage oscillating at a given frequency (let's say the frequency is f). Each plate has a surface area equal to S [m^2]. This is shown in Figure 1:
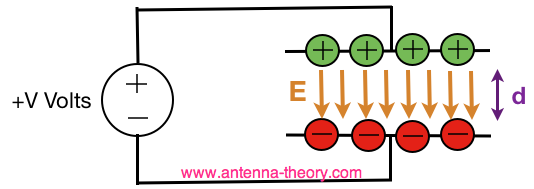 Figure 1. Voltage Across a Parallel Plate Capacitor.
The Capacitance for this parallel plate capacitor can be calculated for this structure. Recall that capacitance is simply the ratio of the charge on the capacitor plates to the voltage across the plates. The result can be found:
In Equation [1], We see from Equation [1] that if the distance between the plates (d) is decreased, the capacitance will increase. This is because the Electric Fields will be stronger, and capacitance is related to stored energy within the Electric Fields. If the Surface Area of the plates is increased, the capacitance will also increase. This is because there will be more area for the Electric Fields to exist in, and hence more energy. Equation [1] represents the fundamental capacitance equation. From it we can understand how to increase or decrease the capacitance of an object. In antenna theory, capacitance is generally bad for radiation, because stored energy does not radiate. Often then, parasitic (or unwanted) capacitance should be reduced. From Equation [1], we know methods of decreasing capacitance: (1) Lower the dielectric constant of the material within the capacitor (2) Increase the separation between the conductive materials that make up the capacitor (3) Decrease the metallic surface area of the capacitor These 3 rules constitute all you need to know about increasing or decreasing capacitance. Voltage and Current Relationships for Capacitors
For inductors, we saw that nature worked to "undo" a loss of flux (magnetic field) within the inductor by inducing an electric current within the inductor coil to counter this loss. Similarly, capacitors don't like to lose Electric Field within the capacitor and the charge can be thought to opposse this change. This isn't quite rigorous, and the real reason comes from Maxwell's Equations, which we will get to later. But the final thing we must know about capacitance is the voltage/current relationship for a capacitor with capacitance C:
Equation [1] states that the current through a capacitor is proportional to the rate of change of the voltage across the capacitor. Hence, a d.c. voltage across a capacitor gives no current - and a rapidly changing voltage (high frequency voltage) gives rise to a relatively large amount of current through the capacitor. Note that there is no conductive path between the plates, and yet current still flows. This electric current is known as Displacement Current. In the next section, we'll look at the fundamental rules for Electric Fields, along with their boundary conditions. Next: Electric Field Rules Top: Capacitance Topics Related To Antenna Theory Antenna Tutorial (Home)
|

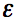 is the
is the 