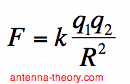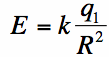Electromagnetics
| Electric Charge | Electric Field | Magnetic Field | Antennas (Home) |
| Lenz's Law | Inductance | Capacitance | E-Field Conditions |
| H-Field Conditions |
|
Electromagnetics is the study of Electric Fields and Magnetic Fields. The subject of electromagnetics seems like a very complicated subject. In college (University), the subject is taught in the 3rd year of most college degree programs (in both electrical engineering and physics). The subject is typically taught with a lot of calculus and spherical coordinate systems. Now, I have a Ph.D. in antenna engineering along with a bunch of industry experience as an engineer. It occurs to me that I never use the complicated math that was used to teach the subject. As such, I will write this electromagnetics tutorial using a minimum of math. I will try to only discuss the concepts I feel have been useful; and I will aim for an intuitive understanding of the subject instead of mathematical manipulations. Electric Charge
The first thing to know in the world of electromagnetism is that there exists electric charge. The universe is made up of atoms, which contain neutrons (electrically neutral or no charge), protons (positive electric charge) and electrons (with negative electric charge). You don't really need to know where charge arises from or what it is, just that charge exists, and there is positive charge and negative charge. Also, charge is measured in Coulombs [C]. Now, we get to the first rule of electromagnetics: charges exert a force on each other. Imagine we have two charges, with charge 1 having q1 Coulombs and charge 2 having q2 Coulombs. What is the force exerted by the charges? I have to throw out an equation, but I'll state what it means in English after:
In Equation [1], k is a universal constant, equal to 8.99*10^9 [N-m^2/C^2], and R is the distance between the two charges. Equation [1] tells us some simple things:
One more fun fact: positive charges repel each other, negative charges repel each other, and positive and negative charges attract. The following Figure illustrates the force relationship:
 Figure 1. Illustration of the Force Equation for Electric Charges.
That is about all we need to know right now about electric charge: it exists, it is either positive or negative, and it exerts a force on other charges. But now that we know about the force equation, we can define the Electric Field.
The Electric Field
The discussion of antennas is about radiated or received waves, and these waves are made up partly of the Electric Field. So it would be a good idea if we know what an electric field is. The Electric Field is defined as the force per unit charge. In simple terms, this means that the Electric Field is the amount of force a charge of +1 Coulomb would experience due to other surrounding charges. Hence, the Electric Field (E-field) due to a charge of q1 [C] would be:
The electric field is actually a vector quantity. This means that the E-field has a magnitude and a direction. Equation [2] gives the magnitude of the Electric Field due to a charge q1 a distance R from the charge. The direction of the Electric Field is directly towards the charge if q1 is negative, and away from the charge if q1 is positive. We can illustrate the Electric Field for a positive and negative charge in Figure 2:
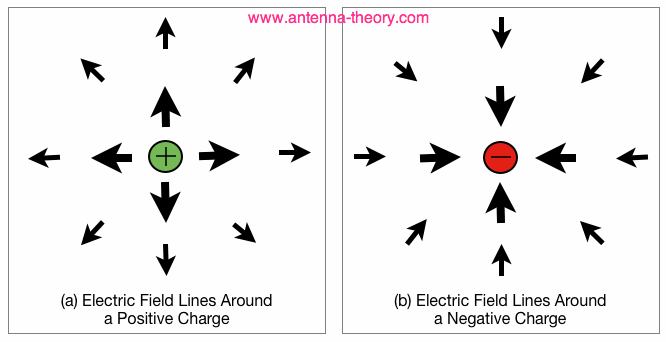 Figure 2. Electric Field Lines Surrounding (a) Positive Point Charge, and (b) Negative Point Charge.
Note that the magnitude of the Electric Field always points directly towards or away from the point charge, and that the magnitude decreases as the you move farther from the charge. Since the E-field is a force per charge, the units are N/C [Newtons per Coulomb]. Since the E-field is so important, we'll define it in a separate way. Suppose a d.c. voltage +V is applied across a capacitor, with separation between the plates d, as shown in Figure 3:
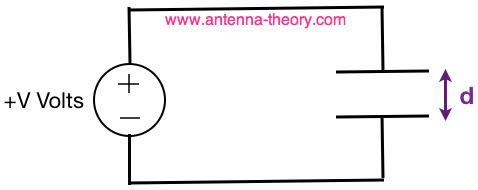 Figure 3. A voltage of +V volts is applied across a parallel plate capacitor with separation d meters.
Recall the relationship between charge (q) and voltage (V) across a capacitor (C) is q=CV. (We will talk more about capacitance in a few pages.) From q=CV, we know that the voltage across the capacitor is equivalent to a buildup of positive charge on the top side of the capacitor in Figure 3 and a negative charge buildup on the lower side of the capacitor. These charges then give rise to - an Electric Field! Hence, the Electric Field direction is shown in Figure 4:
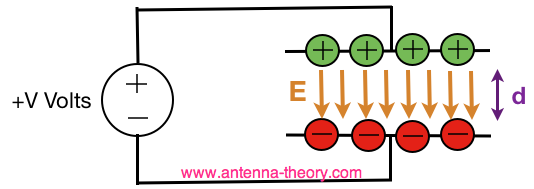 Figure 4. The Electric Fields within a Parallel Plate Capacitor.
It turns out that Newtons/Coulomb is exactly equivalent to Volts/meter. That is, if you have a voltage V across two plates a distance d apart, you can calculate the electric field to be E = V/d. If you work through the math of figuring out the charge on the plates, and then calculate the Electric Field within the plates, you will get the same result. Hence, the Electric field is a measure of how quickly the voltage is changing in space. Equivalently, the Electric Field is a measure of the force a single charge would experience if placed somewhere in space. As a corollary, you can determine the Voltage between two points as the integration (summation) of the Electric Field along a path connecting the points.
Next: Magnetic Fields Top: Introduction to Electromagnetics Topics Related To Antenna Theory Antennas Tutorial (Home)
|