Electric Field Boundary Conditions
| Electric Charge | Electric Field | Magnetic Field | Antennas (Home) |
| Lenz's Law | Inductance | Capacitance | E-Field Conditions |
| H-Field Conditions |
|
Electric Fields obey certain rules. On this page, we'll give these rules. It is important to have a good understanding of these. The electric field distribution around a complex antenna or structure can be understood somewhat intuitively by understanding the rules. First, we'll discuss the Electric Field on the surface of a perfect electric conductor (known as a PEC). Note that for practical purposes, most metals (copper, aluminum, steel, etc) can be considered PECs.
Electric Fields on a Metal or Conductive SurfaceThe Electric Field on any surface can be decomposed into two parts:
The parts of the E-field are illustrated in Figure 1:
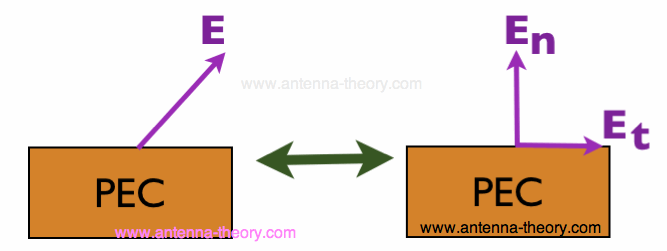 Figure 1. Any Electric Field on the surface of a PEC (left) can be broken into a tangential E-field (Et) and a normal E-field (En) (right).
To discuss the boundary conditions for the Electric Field near a metallic surface, let's first discuss metal.
Metal CharacteristicsFrom an electromagnetics viewpoint, metal is characterized as having a very high conductivity. This means that a small voltage across the metal will produce a huge current. That is, metal has very little electrical resistance, the very reason it is used in wires. Practically, we can assume metal has an infinite conducitivity, and therefore zero resistance. As far as we are concerned, we can assume metal has an infinite number of protons and electrons swimming around in the surface, with zero resistance to them moving. As a result, we can apply no voltage across a metal, because the current would be infinite and your battery or voltage source would break.
Tangential Electric Field Across a MetalLet's discuss what happens when a tangential electric field exists across a metal. For the moment, assume that two charged particles exist near a metallic surface to produce a tangential Electric Field, as shown in Figure 2:
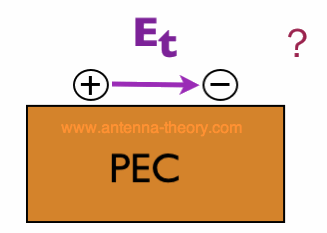 Figure 2. What will happen to a tangential E-field on a PEC?.
What will happen in Figure 2? Since the metal has no resistance to charge flow, negative charge will be attracted to the positive charge, and vice versa. This will work to produce an Electric Field exactly opposite of Et, as shown in Figure 3:
 Figure 3. The free charge in the PEC cancels any tangential E-field.
Figure 3 shows us our first result: Et=0 (always). That is, the tangential Electric Field will always be zero on a metal surface. This is because the free charge will swim around and cancel it out, simply by the attractive nature of charge. And that is cool.
Normal Electric Field On a MetalWhat can we say about the normal component of the Electric Field En? We know that charge gives rise to an Electric Field, that is rule #1 in electromagnetics. And you will have to just accept it that the world of electromagnetics loves symmetry - if current produces a magnetic field then magnetic fields produce currents, reciprocity for antennas, .... Hence, a normal Electric Field will exist on the surface of a PEC only if their exists equivalent charge to produce that Electric Field. This is shown in Figure 4:
 Figure 4. The normal Electric Fields En must exist with Surface Charge on the Metal Surface.
Figure 4 shows that the normal E-field En must exist with an accompanying surface charge. The surface charge is positive if the E-field points away from the surface and negative if the E-field points towards the surface. The surface charge is measured in Coulombs/meter^2 [C/m^2]. The E-field can be directly related to this surface charge, along with the permittivity of the medium surrounding the metal, by:
Electric Field Within a Metal
The Electric Field inside a metal or PEC is always zero (E=0). Always. The reason again follows
from the free charge flow idea used in showing the tangential Electric Field across a metal is zero.
You may recall Ohm's Law for circuits, which states that the Voltage and Current are related by the
resistance of a device. This actually is derived from Electromagnetics, where conductivity
Since the conductivity is infinite, if an electric field existed within the material, the current would be infinite. This can't happen.
Now we have a pretty good idea of how the Electric Field behaves near, in and around a metal. We can now discuss general boundary conditions for the Electric Field (not perfect metals). Suppose we have two regions of space, and these regions have distinct permittivities and conductivities, as seen in Figure 5. How can we relate the Electric Fields at the material boundary?
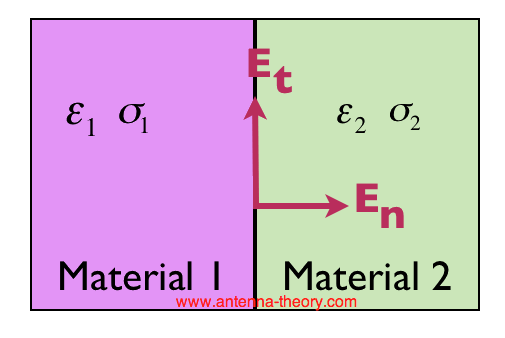 Figure 5. How are the Electric Fields related at a material Discontinuity?.
To put the question in another way, if we know what the fields are on one side of the boundary, how do these relate to the fields immediately on the other side of the boundary? The answer, is known as the rules for the boundary conditions of Electric Fields. The first rule: the tangential Electric Field is equal on the boundary. That is:
Equation [3] states that there is no discontinuity in the tangential electric field crossing a boundary. [Why is this true? The proof is the same as in Kirchoff's Voltage Law for Circuits: The voltage must end up the same after travelling around any two paths in a circuit; similarly the E-field (related to voltage) needs to be the same if you make an imaginary loop around the boundary. But the proof is less important than the result.] What about the normal (perpendicular) component of the Electric Fields (En)? Well, in the absence of any electric charge on the border it just so happens that the Electric Flux Density (D) is continuous (note that D and E are related by the permittivity):
If there is charge at the material discontinuity, then the boundary condition will be affected by the surface charge
density (
And there you have it. These are the fundamental rules of the Electric Field along material interfaces, with particular emphasis paid to how they act around metallic regions.
Next: Magnetic Field Rules Top: Electric Field Rules Topics Related To Antenna Theory Antenna Tutorial (Home)
|

 (the inverse of resistivity)
relates the Electric Field (like Voltage) to the Electric Current Density:
(the inverse of resistivity)
relates the Electric Field (like Voltage) to the Electric Current Density: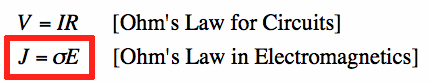

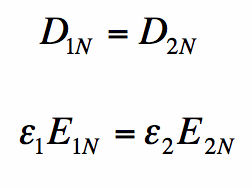
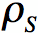 ) [in C/m^2]:
) [in C/m^2]:
