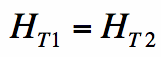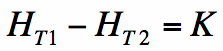Magnetic Field Boundary Conditions
| Electric Charge | Electric Field | Magnetic Field | Antennas (Home) |
| Lenz's Law | Inductance | Capacitance | E-Field Conditions |
| H-Field Conditions |
|
Just as the electric field obeys certain rules, the magnetic field (H-field) also obeys certain rules along the boundary of two different materials. And again, the rules depend on whether we are discussing the tangential component (Ht) or the normal/perpendicular component (Hn) to a surface.
Now, just as there exists the parameter "permittivity" that is associated with electric fields, there exists
an analogous parameter for magnetic fields - permeability,
written by the symbol Back to our material boundary, which we illustrate in Figure 1:
 Figure 1. Illustration of a Material Boundary, along with the Tangential and Perpendicular Magnetic Fields.
The rules are very similar to the Electric Field boundary condition case. First, since there is no such things as magnetic charge, we will have the normal component of the magnetic flux density (B) continuous across a boundary:
Equation [1] states that the component of the magnetic flux density that is perpendicular to the material change is continuous across
the boundary. That is, the vector Bn1 (normal component of B immediately inside region 1) is equal to the vector Bn2 (normal component
of B immediately inside region 2). And since B and H are related by the permeability, we know how the normal component
of the magnetic field Hn changes across the boundary. Note that it doesn't matter what the conductivities (
For the tangential magnetic field (Ht) at a material discontinuity, it is a little more tricky. Recall that magnetic fields are created due to electric current flowing. Hence, if no electric current is flowing on the surface (I=0), then the magnetic field will be continuous across a material boundary change:
Suppose current is flowing on the surface. Then this must give rise to it's own magnetic field on the surface, thus making the magnetic fields (Ht1 and Ht2) discontinuous? Right you are. In that case, we write the surface current as K, which has units of Amps/meter. This is illustrated in Figure 2:
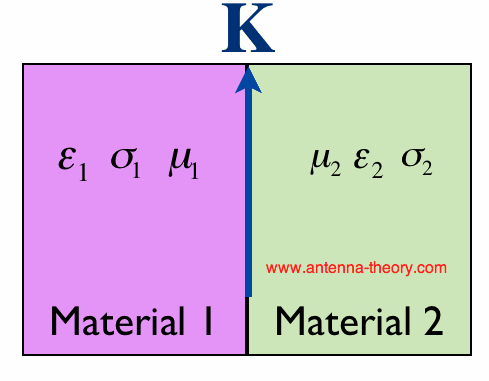 Figure 2. A Boundary Between Two Materials, with a Surface Current Flowing on the Boundary.
In this case, we will have the magnetic field discontinuous by the exact amount of surface current:
Equation [3] states that the tangential component of the magnetic field will be discontinous by the amount of surface current at the boundary (K). That is, Ht1 is the component of the magnetic field tangnetial to the material boundary just inside the region 1. This will differ from Ht2 (the tangential magnetic field just inside region 2) only if an electric current flows on the surface. In the next section, we'll look at how the E- and H- fields interact with each other.
Top: Magnetic Field Boundary Conditions Topics Related To Antenna Theory Antenna Tutorial (Home)
|
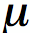 .
This is a property of a material which basically
describes how a material concentrates magnetic fields. The units are measured in Henries/meter [H/m], which is a measure of inductance
over a length.
.
This is a property of a material which basically
describes how a material concentrates magnetic fields. The units are measured in Henries/meter [H/m], which is a measure of inductance
over a length.
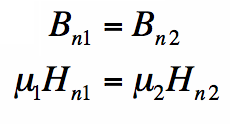
 )
or permittivities (
)
or permittivities (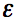 ) are in the two regions - they don't affect the magnetic field's boundary conditions.
) are in the two regions - they don't affect the magnetic field's boundary conditions.