Immittance Charts: More Impedance Matching

On the previous page, the immittance Smith Chart was introduced. On this page, we'll look at more impedance matching examples to illustrate the usefulness of the immittance Smith Chart.

Example 1

In Example 1 on the immittance Smith Chart page, we matched an antenna with impedance z_A=0.1-i*0.2 with a series inductor and a parallel capacitor. What alternatives do we have to match this impedance?

Recall that we moved the impedance z_A to intersect the Re[y]=1 circle with a series inductor. By observing the immittance Smith Chart, we could also accomplish this with a series capacitor. Using a capacitor with a series reactance of -i*0.1, the impedance will be transformed to z1=0.1-i*0.3, which is equivalent to y1=1+i*3. This is illustrated in Figure 1:

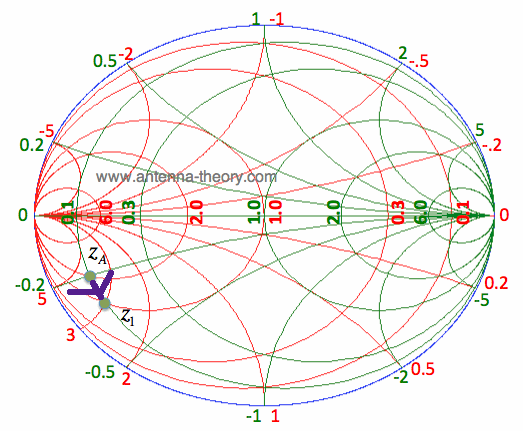Figure 1. Using a Series Capacitor to Move zA to the Re[y]=1 circle.

To complete the impedance matching, we just need to cancel out the susceptance. That is, if we add a parallel inductor with a susceptance of -i*3, the impedance will be translated to the center of the Smith Chart, shown in Figure 2:

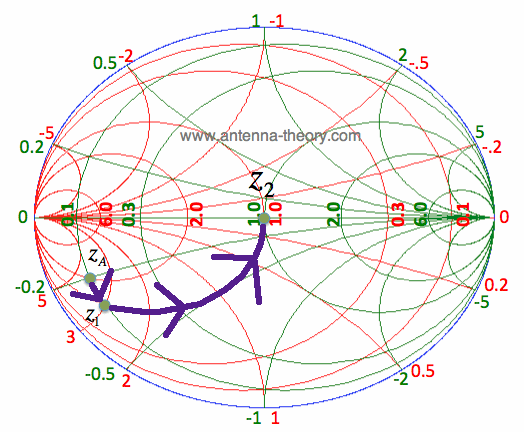Figure 2. A parallel inductor cancels out the susceptance.

This impedance matching network is shown in Figure 3:

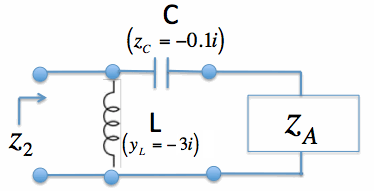Figure 3. The impedance matching network for Example 1.

Hence, we have performed impedance matching using a series capacitor and a parallel inductor; on the previous page this was done with a series inductor and a parallel capacitor.

Example 2

Let's take a look at the impedance z_A = 2 + i*2. In the previous example we did matching with a series component followed by a parallel component. However, if we try to use a series component to move the impedance to intersect the Re[y]=1 or the Re[z]=1 circles, we find we can't do it. Hence, for this impedance we cannot start with a series component.

Which is no big deal, since we can simply use a parallel component to move the impedance to intersect the Re[z]=1 circle. In fact, we have two options here: we can use a parallel capacitor or a parallel inductor to move the impedance to intersect the Re[z]=1 circle. I will use a parallel capacitor.

Note that z_A can be rewritten as y_A = 0.25 - i*0.25. With a parallel capacitor, we will move along the Re[y]=0.25 constant conductance circle. The goal is to intersect the Re[z]=1 constant resistance circle so that we can match with a series component. The intersection of the Re[y]=0.25 and the Re[z]=1 circles occurs at location z1, given by z1 = 1 - i*1.7321. This is equivalent to y1 = 0.25 + i*0.433. Hence, the parallel capacitor required will have a susceptance of yC = y1-y_A = i*0.683, or zC = -i*1.464.

The impedance z1 can then be easily matched with a series inductor with a reactance of zL = i*1.7321. This impedance matching process is shown in Figure 4. Note that for clarity, the circle Re[y]=0.25 and the curve Im[z]=-1.732 is shown. The points and path in Figure 4 should be understood. If not, work through Example 2 and the preceding pages until it is clear.

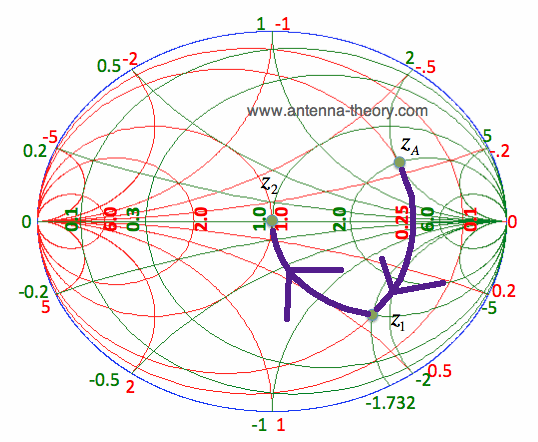Figure 4. Impedance Matching for z_A = 2+i*2.

The impedance matching network for Example 2 is shown in Figure 5.

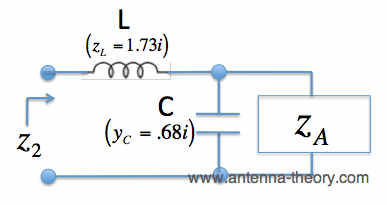Figure 5. Impedance Matching Network for Example 2.

Getting the exact values for the inductors and capacitors is not important. The idea of impedance matching is to understand how the components move you on the Smith Chart, and then get approximate components to perform the matching. Exact values of capacitors and inductors do not exist (i.e. you can find a 0.8 pF capacitor but you can't find a 0.832 pF cap), and the components are non-ideal (some resistance, non-ideal frequency characteristics, etc.), so impedance matching comes down to understanding how components move an impedance on the Smith Chart. Once that is understood, impedance matching is fairly simple.

The Impedance Matching Network Diagram

We saw in Example 1 that the impedance could be matched with a series component followed by a parallel component. In Example 2 we saw that the impedance could be matched with a parallel component followed by a series component. We will now present a graph of the Smith Chart that shows what impedance matching networks are available, in Figure 6:

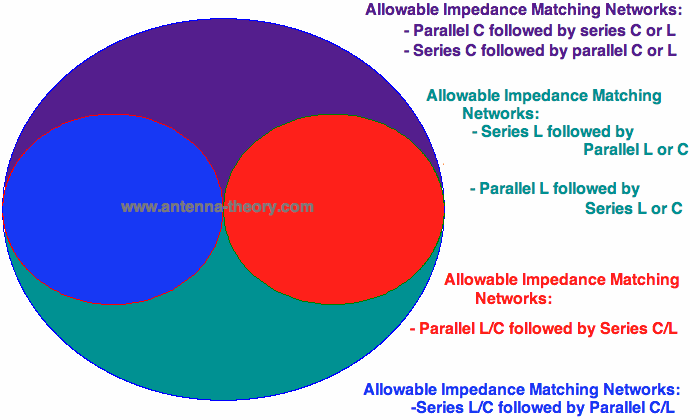Figure 6. Impedance Matching Regions on the Smith Chart.

In the blue region, we only have 2 impedance matching networks possible: a series L followed by a parallel C or a series C followed by a parallel L. In the red region, we can use a parallel L followed by a series C or a parallel C followed by a series L. In the purple region, the first component must be a capacitor. If it is a parallel cap, it must then be followed by a series capacitor or a series inductor, depending on how far the capacitor moved the impedance on the Smith Chart. If a series capaacitor is used as the first matching element in the purple region, then it must be followed by a parallel capacitor or inductor. Similarly, in the green/teal region, the first component must be an inductor.

How do you know which one to use? For single frequency impedance matching, it doesn't matter so much. Large value of inductors are often avoided because they have higher loss, which reduces antenna efficiency. The impedance matching networks are sometimes chosen for what components are readily available.

However, for dual band matching, the type of impedance matching network used will be very important. This is the topic of the next section.