Mathematical Analysis of Waveguides - TM Modes

To understand the magnetic vector potential, note that since the magnetic flux density B must always be divergenceless:

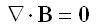If a vector quantity is divergenceless, then it can be expressed as the curl of another vector quantity. In math notation, this means that B can be written as:

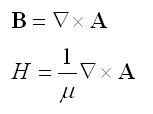In a source free region, it can be shown that A must satisfy the wave equation:

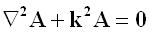In addition, the TMz fields can be found from the Az component of the magnetic vector potential, via the following relationships:

To solve for Az (and hence determine the E- and H- fields), we follow the same procedure as for the TEz case. That is, we use separation of variables and solve the wave equation for the z-component of A, then apply boundary conditions that force the tangential components of the E-fields to be zero on the metallic surfaces. Performing this procedure, which will not be repeated here, we obtain the solution for Az:

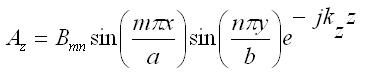        [1]

The corresponding TMz fields for waves propagating in the +z-direction are:

In the above, k is again the wavenumber, and Bmn is a constant, which determines the amplitude of the mn mode (a function of how much power is applied to the waveguide at that frequency).

Before discussing the modes, we must note that TM0n and TMm0 modes cannot exist; that is, m and n must be at least 1. The reason comes from equation [1] above - if either m or n are zero, then Az is equal to zero, so all the fields derived must also be zero. Hence, the lowest order mode for the TM case is the TM11 mode.

The same procedures can be applied from the TE case to determine the cutoff frequencies for the TMmn mode:

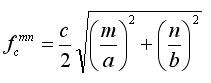Note that the equation for the cutoff frequency is the same for the TE and the TM case. Hence, this confirms that the TE10 mode is the dominant mode for this waveguide. We will conclude this section with the same X-band Rectangular waveguide table as before, displaying the cutoff frequencies for various modes, this time including TM modes.

That's about all you need to know to really understand the TM mode. As in the TE case, if the operating frequency is below the cutoff frequency, then the mode will decay exponentially. If the operating frequency is above the cutoff frequency, propagation will occur for that mode. Note that there is no (1/r) type dependence - that is, the fields do not die off within a waveguide when they propagate.