Waveguide Tutorial
|
Mathematical Analysis of Waveguides Analysis of Waveguide Fields (TE Fields) Analysis of Waveguide Fields (TM Fields)
Introduction to WaveguidesWaveguides are basically a device ("a guide") for transporting electromagnetic energy from one region to another. Typically, waveguides are hollow metal tubes (often rectangular or circular in cross section). They are capable of directing power precisely to where it is needed, can handle large amounts of power and function as a high-pass filter. The waveguide acts as a high pass filter in that most of the energy above a certain frequency (the cutoff frequency) will pass through the waveguide, whereas most of the energy that is below the cutoff frequency will be attenuated by the waveguide. Waveguides are often used at microwave frequencies (greater than 300 MHz, with 8 GHz and above being more common). Waveguides are wideband devices, and can carry (or transmit) either power or communication signals. An example of a hollow metal rectangular waveguide is shown in the following figure.
 Waveguides can bend if the desired application requires it, as shown in the following Figure.  The above waveguides can be used with waveguide to coaxial cable adapters, as shown in the next Figure:
We now know what a waveguide is. Lets examine metal cavities with a rectangular cross section,
as shown in Figure 1. Assume the waveguide is filled with vaccuum, air or some dielectric with
the permeability given by
The waveguide has a width a in the x-direction, and a height b in the y-direction, with a>b. The z-axis is the direction in which the waveguide is to carry power.
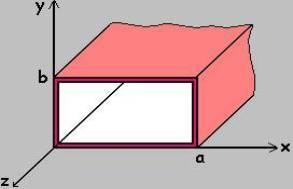 Figure 1. Cross section of a waveguide with long dimension a and short dimension b. On this page, I'm going to give the general "rules" for waveguides. That is, I'll give the equations for key parameters and let you know what the parameters mean. On the next page, we'll go into the mathematical derivation (which you would do in engineering graduate school), but you can get away with not knowing all that math if you don't want to know it. First and possibly most importantly, this waveguide has a cutoff frequency, fc. The cutoff frequency is the frequency at which all lower frequencies are attenuated by the waveguide, and above the cutoff frequency all higher frequencies propagate within the waveguide. The cutoff frequency defines the high-pass filter characteristic of the waveguide: above this frequency, the waveguide passes power, below this frequency the waveguide attenuates or blocks power. The cutoff frequency depends on the shape and size of the cross section of the waveguide. The larger the waveguide is, the lower the cutoff frequency for that waveguide is. The formula for the cutoff frequency of a rectangular cross sectioned waveguide is given by:
In the above, c is the speed of light within the waveguide, mu is the permeability of the material that fills the waveguide, and epsilon is the permittivity of the material that fills the waveguide. Note that the cutoff frequency is independent of the short length b of the waveguide. The cutoff frequency for a waveguide with a circular cross section of radius a is given by:
 Due to Maxwell's Equations, the fields within the waveguide always have a specific "form" or "waveshape" to them - these are called modes. Assume the waveguide is oriented such that the energy is to be transmitted along the waveguide axis, the z-axis. The modes are classified as either TE ('transverse electric' - which indicates that the E-field is orthogonal to the axis of the waveguide, so that Ez=0) or TM ('transverse magnetic' - which indicates that the H-field is orthogonal to the axis of the waveguide, so Hz = 0). The modes are further classified as TEij, where the i and j indicate the number of wave oscillations for a particular field direction in the long direction (dimension a in Figure 1) and short direction (dimension b in Figure 1), respectively. Metal waveguides cannot support the TEM ('transverse electric and magnetic' - when Ez and Hz are zero) mode. Their exists no solution to Maxwell's equations that also satisfy the required boundary conditions for this mode to occur. Unfortunately, at this point we can't say too much more about waveguides without getting into the mathematical derivation. For practicing engineers, this often isn't required. However, if you're interested, move on to the next page.
Up: Waveguides Topics Related To Antenna Theory Antenna Tutorial (Home)
|
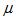and the
.