Mathematical Analysis of Waveguides
|
In this section, we will take a mathematical look at waveguides and derive some of their key properties.
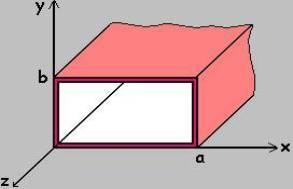
We will again be concerned with metal (perfectly conducting) waveguides with a rectangular cross section
as shown in Figure 1.
If you weren't aware, electromagnetics is governed by Maxwell's Equations, and Maxwell's Equations are not easy to solve. Hence, every math trick someone can think of will be used in order to make the analysis tractable. We'll start with discussing the electric vector potential, F. In a source-free region (i.e., an area through which waves propagate that is away from sources), we know that:
 In the above, D is the Electric Flux Density. If a vector quantity is divergenceless (as in the above), then it can be expressed as the curl of another quantity. This means that we can write the solution for D and the corresponding electric field E as:
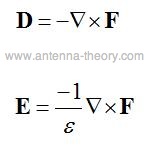 In the above, epsilon is the permittivity of the medium through which the wave propagates. We are purely in the world of mathematics now. The quantity F is not physical, and is of little practical value. It is simply an aid in performing our mathematical manipulations. It turns out that waves (or electromagnetic energy) can not propagate in a waveguide when both Hz and Ez are equal to zero. Hence, what field configurations that are allowed will be classified as either TM (Transverse Magnetic, in which Hz=0) and TE (Transverse Electric, in which Ez=0). The reason that waves cannot be TEM (Transverse Electromagnetic, Hz=Ez=0) will be shown towards the end of this derivation. To perform our analysis, we'll assume that Ez=0 (i.e., we are looking at a TE mode or field configuration). In this case, working through Maxwell's equations, it can be shown that the E- and H- fields can be determined from the following equations:
 Therefore, if we can find Fz (the z-component of the vector F), then we can find the E- and H- fields. In the above equation, k is the wavenumber. Working through the math of Maxwell's Equations, it can be shown that in a source-free region, the vector potential F must satisfy the vector wave equation:
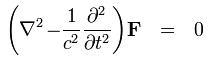 [1] [1]To break this equation down, we will look only at the z-component of the above equation (that is, Fz). We will also assume that we are looking at a single frequency, so that the time dependence is assumed to be of the form given by (we are now using phasors to analyze the equation):
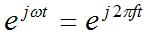 Then the equation [1] can be simplified as follows:
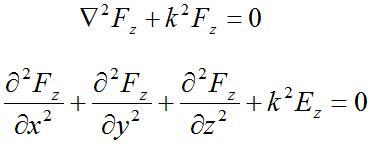 [2] [2]To solve this equation, we will use the technique of separation of variables. Here we assume that the function Fz(x, y, z) can be written as the product of three functions, each of a single variable. That is, we assume that:
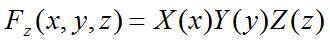 [3] [3](You might ask, how do we know that the separation of variables assumption above is valid? We don't - we just assume its correct, and if it solves the differential equation when we are done doing the analysis then the assumption is valid). Now we plug in our assumption for Fz (equation [3]) into equation [2], and we end up with:
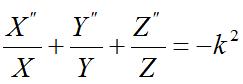 [4] [4]In the above equation, the prime represents the derivative with respect to the variable in the equation (for instance, Z' represents the derivative of the Z-function with respect to z). We will break up the variable k^2 into components (again, just to make our math easier):
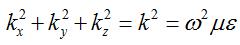 [5] [5]
Using equation [5] to breakdown equation [4], we can write:
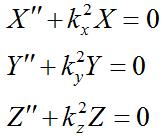 [6] [6]The reason that the equations in [6] are valid is because they are only functions of independent variables - hence, each equation must hold for [5] to be true everywhere in the waveguide. Solving the above equations using ordinary differential equations theory, we get:
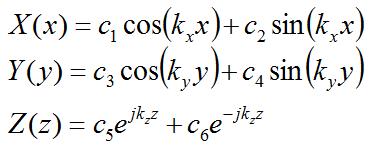 [7] [7]The form of the solution in the above equation is different for Z(z). The reason is that both forms (that for X and Y, and that for Z), are both equally valid solutions for the differential equations in equation [6]. However, the complex exponential typically represents travelling waves, and the [real] sinusoids represent standing waves. Hence, we choose the forms given in [7] for the solutions. No math rules are violated here; again, we are just choosing forms that will make our analysis easier. For now, we can set c5=0, because we want to analyze waves propagating in the +z-direction. The analysis is identical for waves propagating in the -z-direction, so this is fairly arbitrary. The solution for Fz can be written as:
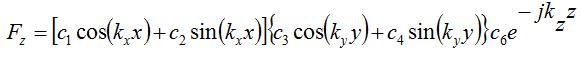 [8] [8]
If you remember anything about differential equations, you know there needs to be some boundary
conditions applied in order to determine the constants. Recalling our physics, we know that
the tangential Electric fields at any perfect conductor must be zero (why? because
The tangential fields must be zero, so Ex must be zero when y=0 and when y=b (see Figure 1 above), no matter what the value for y and z are. In addition, Ey must be zero when x=0 and when x=a (independent of x and z). We will calculate Ex:
 Ex is given by the above equation. The boundary condition given by
implies that c4 must be equal to zero. This is the only way that boundary condition given in [9] will be true for all x and z positions. If you don't believe this, try to show that it is incorrect. You will quickly determine that c4 must be zero for the boundary condition in [9] to be satisfied everywhere it is required. Next, the second boundary condition,
implies something very unique. The only way for the condition in [10] to be true for all values of x and z whenever y=b, we must have:
 If this is to be true everywhere, c3 could be zero. However, if c3 is zero (and we have already determined that c4 is zero), then all of the fields would end up being zero, because the function Y(y) in [7] would be zero everywhere. Hence, c3 cannot be zero if we are looking for a nonzero solution. Hence, the only alternative is if the above equation implies that:
 This last equation is fundamental to understanding waveguides. It states that the only solutions for Y(y) function must end up being sinusoids, that an integer number of multiples of a half-wavelength. These are the only type of functions that satisfy the differential equation in [6] and the required boundary conditions. This is an extremely important concept. If we invoke our other two boundary conditions:
Ey(x=a, y, z)=0 Then (using identical reasoning to that above), we can determine that c2=0 and that:
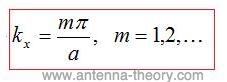 This statement implies that the only functions of x that satisfy the differential equation and the required boundary conditions must be an integer multiple of half-sinusoids within the waveguide. Combining these results, we can write the solution for Fz as:
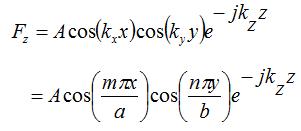 In the above, we have combined the remaining nonzero constants c1, c3, and c6 into a single constant, A, for simplicity. We have found that only certain distributions (or field configurations) will satisfy the required differential equations and the boundary conditions. Each of these field configurations will be known as a mode. Because we derived the results above for the TE case, the modes will be known as TEmn, where m indicates the number of half-cycle variations within the waveguide for X(x), and n indicates the number of half-cycle variations within the waveguide for Y(y). In the next section, we'll explicitly write out the fields corresponding to these modes, discuss which modes are allowable, and look into the TM (transverse magnetic) case.
|
Previous: Intro to Waveguides
Waveguides (Main)
Topics Related To Antenna Theory
Antenna Tutorial (Home)
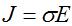 , so if the conductivity approaches infinity (perfect conductor),
then if the tangential E-field is not zero then the induced current would be infinite).
, so if the conductivity approaches infinity (perfect conductor),
then if the tangential E-field is not zero then the induced current would be infinite).