Mathematical Analysis of Waveguides (Continued)
|
On the previous page,
the z-component of the electric vector potential for the TE mode was derived:
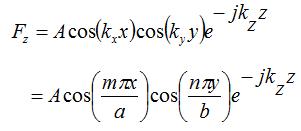 Using the field relationships:
 We can write the allowable field configurations for the TE (transverse electric) modes within a waveguide:
 In the above, the constants are written as Amn - this implies that the amplitude for each mode can be independent of the others; however, the field components for a single mode must all be related (that is, Ex and Hy do not have independent coefficients).
Cutoff Frequency (fc)At this point in the analysis, we are able to say something intelligent. Recall that the components of the wavenumber must satisfy the relationship:
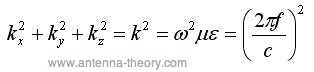 [3] [3]Since kx and ky are restrained to only take on certain values, we can plug this fact in:
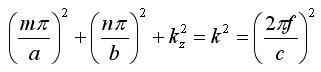 [4] [4]An interesting question arises at this point: What is the lowest frequency in which the waveguide will propagate the TE mode?
For propagation to occur, To find the lowest frequency in which propagation can occur, we set kz=0. This is the transition between the cutoff region (evanescent) and the propagation region. Setting kz=0 in equation [4], we obtain:
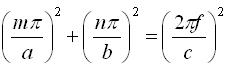 [5] [5]
If m and n are both zero, then all of the field components in [1-2] become zero, so we cannot have this condition. The lowest value the left hand side of equation [5] can take occurs when m=1 and n=0. The solution to equation [5] when m=1 and n=0, gives the cutoff frequency for this waveguide:
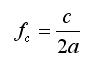 Any frequency below the cutoff frequency (fc) will only result in evanescent or decaying modes. The waveguide will not transport energy at these frequencies. In addition, if the waveguide is operating at a frequency just above fc, then the only mode that is a propagating mode will be the TE10 mode. All other modes will be decaying. Hence, the TE10 mode, since it has the lowest cutoff frequency, is referred to as the dominant mode. Every mode that can exist within the waveguide has its own cutoff frequency. That is, for a given mode to propagate, the operating frequency must be above the cutoff frequency for that mode. By solving [5] in a more general form, the cutoff frequency for the TEmn mode is given by:
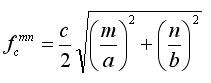 Although we haven't discussed the TM (transverse magnetic) mode, it will turn out that the dominant TM mode has a higher cutoff frequency than the dominant TE mode. This will be discussed in the next section. To give an example of the cutoff frequencies of various modes, let's consider a standard x-band waveguide, with dimensions of a=0.9" (2.286 cm) and b=0.4" (1.016 cm). Assuming the waveguide is filled with air (or a vacuum), then the cutoff frequencies for various modes are given in the following table:
If we are running a signal that is centered around 15 GHz with a 1 GHz bandwidth, then the only TE modes that would propagate would be TE10, TE20 and TE01. In the next section, we'll look at the TM mode.
|
Previous: Mathematical Analysis of Waveguides 1
Waveguides (Table of Contents)
Antenna Theory (Home)
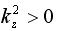 .
If this is true, then kz is a real number, so that the field components (equations [1] and [2]) will
contain complex exponentials, which represent propagating waves. If on the other hand,
.
If this is true, then kz is a real number, so that the field components (equations [1] and [2]) will
contain complex exponentials, which represent propagating waves. If on the other hand,
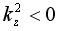 , then kz will be an imaginary number, in which
case the complex exponential above in equations [1-2] becomes a decaying real exponential.
In this case, the fields
will not propagate but instead quickly die out within the waveguide. Electromagnetic fields
that die off instead of propagate are referred to as evanescent waves.
, then kz will be an imaginary number, in which
case the complex exponential above in equations [1-2] becomes a decaying real exponential.
In this case, the fields
will not propagate but instead quickly die out within the waveguide. Electromagnetic fields
that die off instead of propagate are referred to as evanescent waves.