Smith Chart Tutorial - Load Transformation
|
On this page, we'll see how the Smith Chart makes viewing the impedance transformation due to transmission lines
very simple. That is, suppose that we have an impedance ZL on the end of a
transmission line with
characteristic impedance given by Z0, as shown in Figure 1:
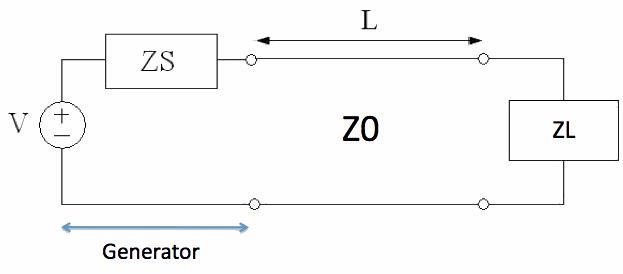 Figure 1. Diagram of a Load Impedance at the End of a Transmission Line. In Figure 1, we have a load impedance (which could represent an antenna, for instance), attached to a generator (or voltage source, with source impedance ZS) via a transmission line of length L and characteristic impedance Z0. To find the input impedance a distance L from the load ZL, we can use the complicated equation found in the transmission line tutorial:
 [1] [1]
(Recall that Now, the question is: If we have a load impedance ZL, what is the input impedance Zin a distance L down the transmission line, using the Smith Chart? To figure this out, let's just take an example. Let ZL = 100 Ohms, so that the normalized load is zL=100/50 = 2.0. Let's plot, on the Smith Chart, a few values for zin=Zin/Z0, which are given by:
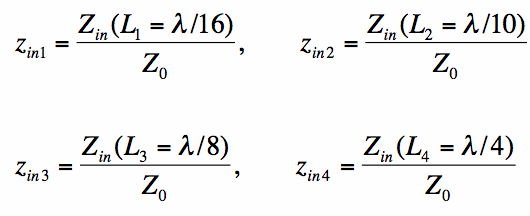 [2] [2]We can calculate the input impedances using equation [1]:
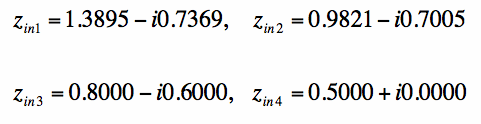 [3] [3]The impedances in equation [3] are plotted in Figure 2:
 Figure 2. Input Impedances of Equation [3] Plotted on the Smith Chart. From Figure 2, something interesting emerges. We could go through a ton of math equations to prove this, but that's not real fruitful. Each of the points in Figure 2 are the same distance away from the center of the Smith Chart. That is, the complicated input impedance equation ([2] above) translates into a simple circular motion on the Smith Chart. Hence, you can find the impedance of a load a distance L down a transmission line simply by moving in a circular fashion around the Smith Chart. Let's take an example. Let zL = 2.0 again as above. If we draw a circle centered at the center of the Smith Chart and travelling through zL, then we get the curve given in Figure 3 by the black x's:
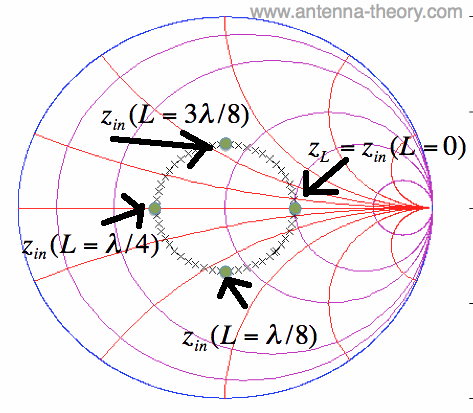 Figure 3. Constant VSWR circle.
The circle in Figure 3 that runs through zL is known as a constant VSWR or constant SWR circle. Since
this circle is centered at the center of the Smith Chart, the magnitude of
ExampleAn example will help cement the above idea. Suppose we know that the input impedance, z1=0.1 (so Z1=0.1*50=5), at location 1 in Figure 4. What is the input impedance of the load, ZL, and Z2 (the impedance at the generator), assuming Z0=50 Ohms?
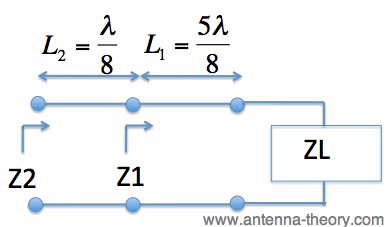 Figure 4. Diagram of Transmission Line Problem. Solution. This problem is very simple thanks to the Smith Chart. First, plot the known value of z1, along with the constant VSWR curve (the circle centered in the Smith Chart going through z1):
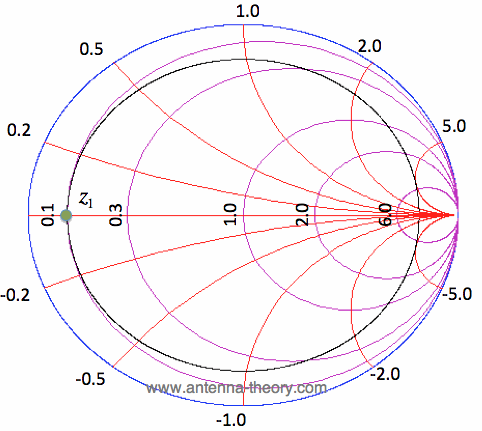 Figure 5. The First Step: Plotting z1 and the Constant VSWR Circle. To determine ZL, we want to move on the Smith Chart towards the load. Remember:
Hence, to find ZL, we want to move in the counter-clockwise direction. Note that L1 = 5*lambda/8. Recall that a distance of lambda/2 on a transmission line corresponds to a complete rotation on the Smith Chart. Hence, this is equivalent to moving 5*lambda/8 - lambda/2 = lambda/8. Hence, we can simply rotate in the counter-clockwise direction by 90 degrees (one quarter turn on the Smith Chart). We can then read off the value for this impedance, and the result is:
Similarly, to find z2, the impedance at the generator, we simply move lambda/8 in the clockwise direction (since we are traveling away from the antenna/load). The result is a 90 degree rotation, plotted in Figure 6. The result is:
The correspond Smith Chart is shown, with only the needed constant resistance circles and constant reactance curves:
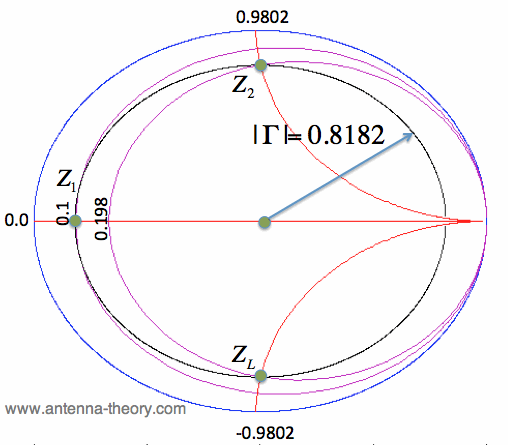 Figure 6. The Second Step: Using the Constant SWR Circle to Get zL and z2.
In Figure 6, the circle corresponds to the magnitude of Finally, on complicated, detailed Smith Charts, you will see a scale along the outer perimeter as shown below:
 In conclusion, this might seem all kind of stupid. But actually it will be very useful for understanding antenna responses at an intuitive level, and to help visualize how impedances change due to transmission lines. More importantly, it is very useful in impedance matching, as we will see.
Previous: Constant Reactance Curves Topics Related To Antenna Theory
|
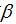 is the
is the 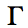 is constant
along this curve. Hence, the
is constant
along this curve. Hence, the