Two Dimensional Phased Arrays
|
In this section, we'll look at two-dimensional or planar arrays with uniform spacing and with
phased weights. Fortunately,
two-dimensional phased arrays are not much more difficult to understand than one-dimensional arrays. In one-dimensional arrays, the weights are chosen to compensate for the phase propagation of a wave in a desired direction. The extension to two-dimensional arrays is straight forward. Lets assume we have an array in the (x,y) plane, with positions given by:
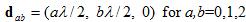 This array is plotted in Figure 1.
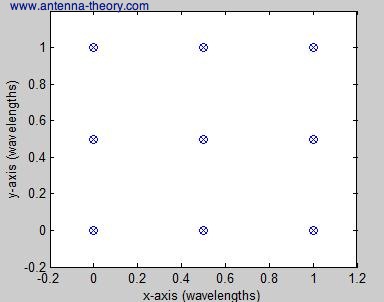 Figure 1. Array geometry for two-dimensional (planar) array.
The phased weights for a two-dimensional planar array steered towards
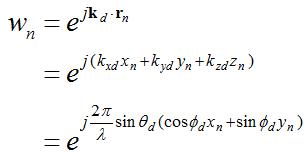
In the above equation, the weights are designed to steer the array towards
the wave vector
in the desired direction, written as
To illustrate this, we'll assume the array is steered to broadside -
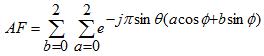 Applying the sum formula twice, the above reduces to:
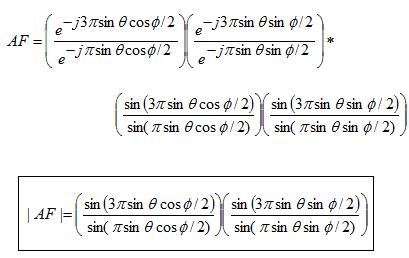 To plot this function, we'll introduce simplifying variables, u and v:
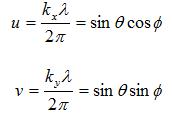 The above variables are often used in plotting two-dimensional patterns, and are known as directional cosines. A plot of the AF above is shown in Figure 2:
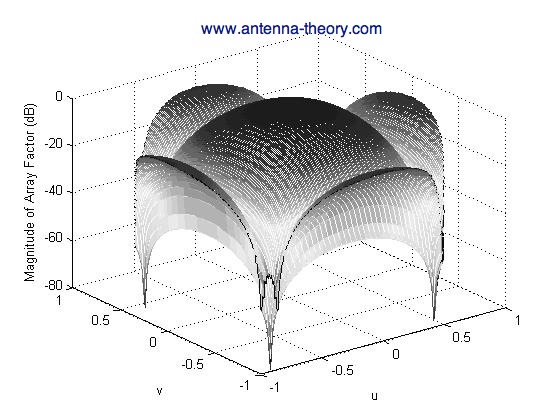 Figure 2. Magnitude of AF for two-dimensional array described above.
As expected, the array is maximum when (u, v)=(0,0), which corresponds to the
desired direction
|
Antenna Weighting Page
Antenna (Home)
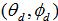 are given by:
are given by: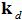 .
. 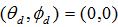 .
In this case, all of the weights simply become equal to unity (1.0). The array factor
becomes:
.
In this case, all of the weights simply become equal to unity (1.0). The array factor
becomes: