Analysis of Uniform Phased Arrays

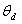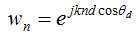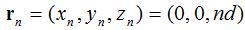
In this page, we'll derive a general equation for the array factor or antenna array response for an N element uniformly spaced linear antenna array. The weights will be simple phased weights; when the antenna array is steered towards direction , the weights are given by: Assuming that element n is at location given by: This implies that the inter-element spacing is constant and equal to d. Our goal now is to determine the response of the array when steered towards , when the weights are chosen using the equation above. 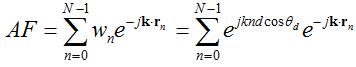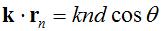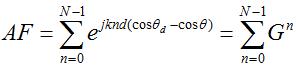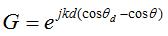Using the definition of the array factor, we can write: The above can be simplified by recalling the definition of the wave vector: Substituting the above equation into the array factor equation, In the above equation, G is a "dummy variable" that is simply given by: Recall the following sum formula, which will make our work simple: 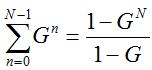The array factor can be rewritten using the above identity as: 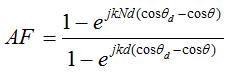Really, we only care about the magnitude of the array factor. Hence, we can factor out terms from the numerator and denominator that will simplify the results when we take the magnitude: 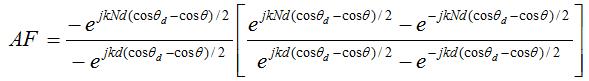Taking the magnitude of the above equation, the multiplying complex exponentials (which always have a magnitude equal to one) go away. In addition, using the following general formula for the sin() function: 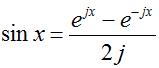The magnitude of the array factor reduces to: 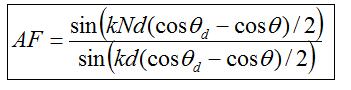In the next section, we'll look at understanding this equation (which explains grating lobes), and extend the results to two-dimensional (planar) antenna arrays.