Dolph-Chebyshev Weights
|
You may have noticed that the antenna
array factors
for arrays with uniform weights have unequal sidelobe levels, as seen
here. Often it is desirable
to lower the highest sidelobes, at the expense of raising the lower sidelobes. The optimal sidelobe
level (for a given beamwidth) will occur when the sidelobes are all equal in magnitude.
This problem was solved by Dolph in 1946. He derives a method for obtaining weights for uniformly
spaced linear arrays steered to broadside ( To understand this weighting scheme, we'll first look at a class of polynomials known as Chebyshev (also written Tschebyscheff) polynomials. These polynomials all have "equal ripples" of peak magnitude 1.0 in the range [-1, 1] (see Figure 1 below). The polynomials are defined by a recursion relation:
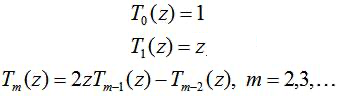 Examples of these polynomials are shown in Figure 1.
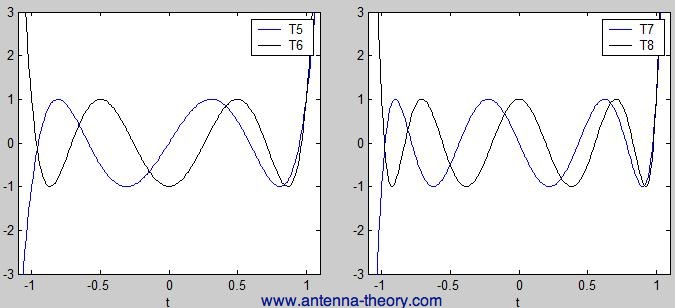 Figure 1. Examples of Chebyshev polynomials. Observe that the oscillations within the range [-1, 1] are all equal in magnitude. The idea is to use these polynomials (with known coefficients) and match them somehow to the array factor (the unknown coefficients being the weights). To begin to see how this is achieved, lets assume we have a symmetric antenna array - for every antenna element at location dn there is an antenna element at location -dn, both multiplied by the same weight wn. We'll further assume the array lies along the z-axis, is centered at z=0, and has a uniform spacing equal to d. Then the array factor will be of the form given by:
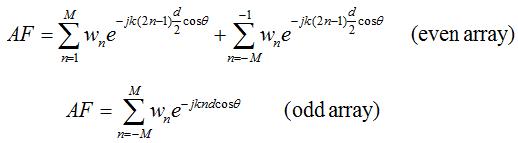 The array is even if there are an even number of elements (no element at the origin), or odd if there are an odd number of elements (an element at the origin). Using the complex-exponential formula for the cosine function:
 The array factors can be rewritten as:
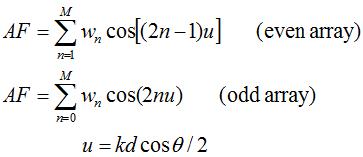 Recall that we want to somehow match this expression to the above Tschebyscheff polynomials in order to obtain an equil-sidelobe design. To do this, we'll recall some trigonometry which states relations between cosine functions:
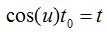
we will end up with an AF that is a polynomial. We can now match this polynomial to
the corresponding Tschebyshef polynomial (of the same order), and determine the corresponding
weights,
The parameter
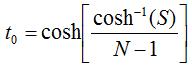 The resulting Array Factor (AF) will have the minimum null-null beamwidth for the specified sidelobe level, and the sidelobes will all be equal in magnitude. In the next section, we'll illustrate this method with an example.
|
Next: More on the Dolph-Chebyshev Method
Antenna Arrays (Main)
Antennas (Home)
 =90 degrees).
This is a popular weighting method because the sidelobe level can be specified, and the minimum possible
=90 degrees).
This is a popular weighting method because the sidelobe level can be specified, and the minimum possible
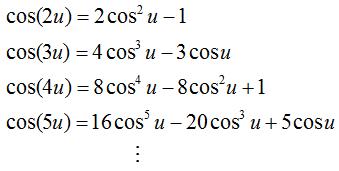
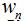 .
.  is used to determine the sidelobe level. Suppose there are N elements in the array,
and the sidelobes are to be a level of S below the peak of the main beam in linear units (note, that
if S is given in dB
(
is used to determine the sidelobe level. Suppose there are N elements in the array,
and the sidelobes are to be a level of S below the peak of the main beam in linear units (note, that
if S is given in dB
(