Smith Charts: Constant Reactance Curves

On this page, we will look at the set of curves defined by zL = R + iY, where Y is held constant and R varies from 0 to infinity. Since R cannot be negative for antennas or passive devices, we will restrict R to be greater than or equal to zero. As a first example, let zL = R + i. The curve defined by this set of impedances is shown in Figure 1:

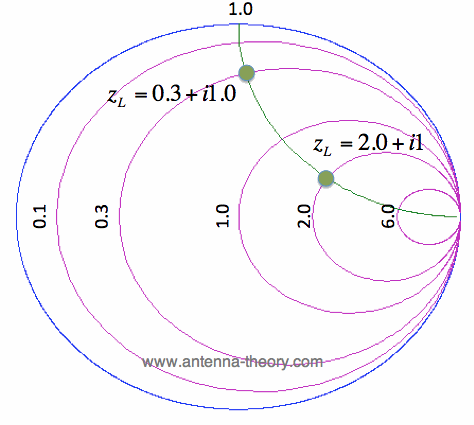Figure 1. Constant Reactance Curve for zL = R + i*1.

The resulting curve zL = R + i is plotted in green in Figure 1. A few points along the curve are illustrated as well. Observe that zL = 0.3 + i is at the intersection of the Re[zL] = 0.3 circle and the Im[zL]=1 curve. Similarly, observe that the zL = 2 + i point is at the intersection of the Re[zL]=2 circle and the Im[zL]=1 curve. (For a quick reminder of real and imaginary parts of complex numbers, see complex math primer.)

The constant reactance curve, defined by Im[zL]=-1 is shown in Figure 2:

Figure 2. Constant Reactance Curve for zL = R - i.

The resulting curve for Im[zL]=-1 is plotted in green in Figure 2. The point zL=1-i is placed on the Smith Chart, which is at the intersection of the Re[zL]=1 circle and the Im[zL]=-1 curve.

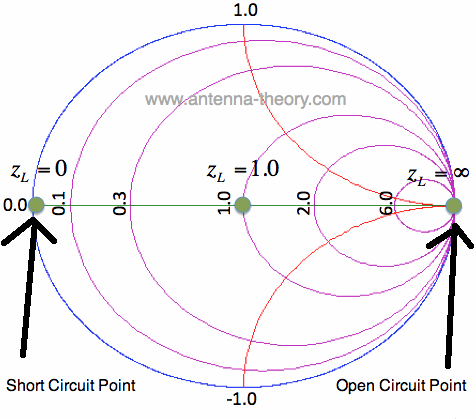Figure 3. Constant Reactance Curve for zL=R.

The reactance curve given by Im[zL]=0 is a straight line across the Smith Chart. There are 3 special points along this curve. On the far left, where zL = 0 + i0, this is the point where the load is a short circuit, and thus the magnitude of is 1, so all power is reflected.

In the center of the Smith Chart, we have the point given by zL = 1. At this location, is 0, so the load is exactly matched to the transmission line. No power is reflected at this point.

The point on the far right in Figure 3 is given by zL = infinity. This is the open circuit location. Again, the magnitude of is 1, so all power is reflected at this point, as expected.

Finally, we'll add a bunch of constant reactance curves on the Smith Chart, as shown in Figure 4.

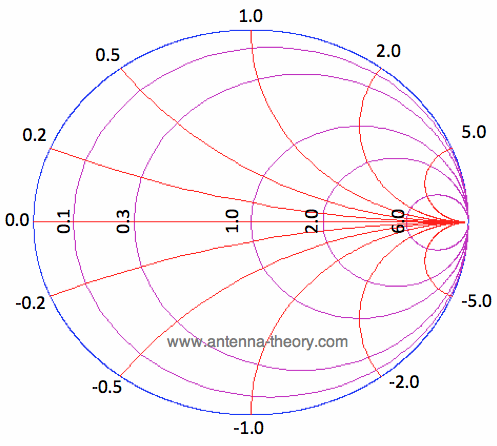Figure 4. Smith Chart with Reactance Curves and Resistance Circles.

In Figure 4, we added constant reactance curves for Im[zL]=2, Im[zL]=5, Im[zL]=0.2, Im[zL]=0.5, Im[zL]=-2, Im[zL]=-5, Im[zL]=-0.2, and Im[zL] = -0.5.

Figure 4 shows the fundamental curves of the Smith Chart. If you look back on Figure 1 on the intro to Smith Charts page, it should now make sense where all the chaotic curves come from.

In the next section, we'll begin to look at some of the things that make Smith Charts so useful.