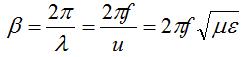Transmission Lines - Models and Characteristic Impedance
|
In this section, we'll form a model for transmission lines and then analyze the equations that govern
their behaviour. We'll then introduce the key property of characteristic impedance. To understand transmission lines, we'll set up an equivalent circuit to model and analyze them. To start, we'll take the basic symbol for a transmission line of length L and divide it into small segments:
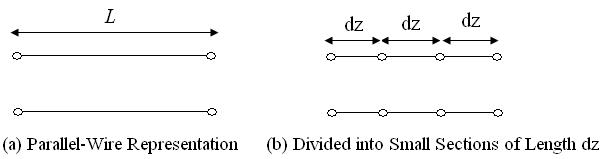 Then we'll model each small segment with a small series resistance, series inductance, shunt conductance, and shunt capcitance:
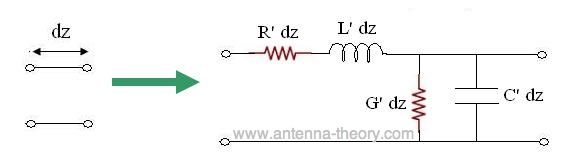 The parameters in the above figure are defined as follows: R' - resistance per unit length for the transmission line (Ohms/meter) L' - inductance per unit length for the tx line (Henries/meter) G' - conductance per unit length for the tx line (Siemans/meter) C' - capacitance per unit length for the tx line (Farads/meter) We will use this model to understand the transmission line. All transmission lines will be represented via the above circuit diagram. For instance, the model for coaxial cables will differ from microstrip transmission lines only by their parameters R', L', G' and C'. To get an idea of the parameters, R' would represent the d.c. resistance of one meter of the transmission line. The parameter G' represents the isolation between the two conductors of the transmission line. C' represents the capacitance between the two conductors that make up the tx line; L' represents the inductance for one meter of the tx line. These parameters can be derived for each transmission line. An example of deriving the paramters for a coaxial cable is given here. Assuming the +z-axis is towards the right of the screen, we can establish a relationship between the voltage and current at the left and right sides of the terminals for our small section of transmission line:
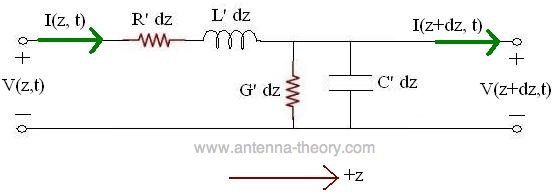 Using oridinary circuit theory, the relationship between the voltage and current on the left and right side of the transmission line segment can be derived:
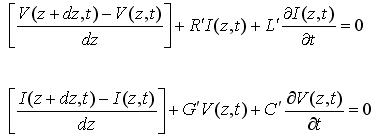 Taking the limit as dz goes to zero, we end up with a set of differential equations that relates the voltage and current on an infinitesimal section of transmission line:
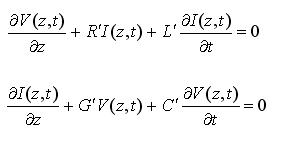 These equations are known as the telegraphers equations. Manipulation of these equations in phasor form allow for second order wave equations to be made for both V and I:
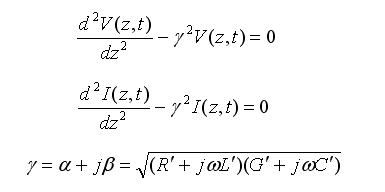 The solution of the above wave-equations will reveal the complex nature of transmission lines. Using ordinary differential equations theory, the solutions for the above differential equations are given by:
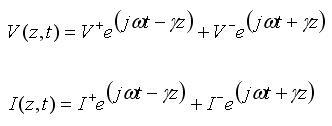
The solution is the sum of a forward traveling wave (in the +z direction) and a backward traveling
wave (in the -z direction). In the above, Characteristic Impedance - Z0We're now ready to introduce a fundamental parameter of every transmission line: its characteristic impedance. This is defined as the ratio of the magnitude of the forward traveling voltage wave to the magnitude of the forward traveling current wave:
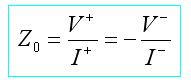 In terms of the transmission line per-length parameters, the characteristic impedance is given by:
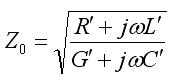 Z0 will be extensively used in determining other transmission line parameters. This page will end with special cases of the characteristic Impedance. If R'=G'=0, then the conductors of the transmission line are perfectly conducting (so R'=0) and the dielectric medium that separates the conductors has zero conductivity (so that G'=0). In this case, the line is referred to as a Lossless Line. The characteristic impedance becomes:
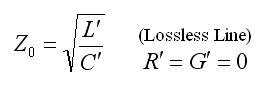 Another type of line of interest is the distortionless line This type of line may contain loss (so that the voltage dies off somewhat as it propagates down the line), but the magnitude of the attenuation is frequency-independent, and the phase constant varies linearly with frequency. This is desirable; similar to filter theory, this would be considered "linear phase" - that is, signals that come out of the transmission line might be attenuated, but have the same shape. The criteria for this is:

The Propagation Constant: |
Previous: Intro to Transmission Lines
Transmission Lines (Table of Contents)
Antennas Tutorial (Home)
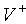 is the amplitude of the forward traveling voltage wave,
is the amplitude of the forward traveling voltage wave, 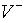 is the amplitude of the backward traveling voltage wave,
is the amplitude of the backward traveling voltage wave,
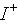 is the amplitude of the forward traveling
current wave, and
is the amplitude of the forward traveling
current wave, and 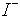 is the amplitude of
the backward traveling current wave.
is the amplitude of
the backward traveling current wave.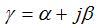
 ; this represents the rate of decay
of the wave as it travels down the transmission line. The larger
; this represents the rate of decay
of the wave as it travels down the transmission line. The larger 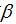 . This represents the
rate at which the waves oscillate as a function of position on the line. In contrast, frequency represents the rate
of change of oscillation as function of time. For a lossless line,
. This represents the
rate at which the waves oscillate as a function of position on the line. In contrast, frequency represents the rate
of change of oscillation as function of time. For a lossless line,