Transmission Lines: Reflection Coefficient and VSWR
|
We are now aware of the characteristic impedance of a transmission line, and that the tx line gives rise to forward and backward travelling voltage and current waves. We will use this information to determine the voltage reflection coefficient, which relates the amplitude of the forward travelling wave to the amplitude of the backward travelling wave. To begin, consider the transmission line with characteristic impedance Z0 attached to a load with impedance ZL:
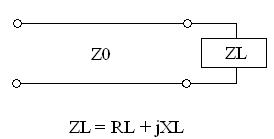
At the terminals where the transmission line is connected to the load, the overall voltage must be given by:
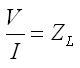 [1] [1]
Recall the expressions for the voltage and current on the line (derived on the previous page):
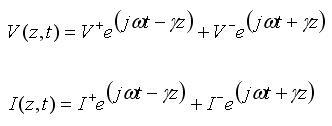 [2] [2]
We want to plug Equation [1] into Equation [2]. Since we can use whatever origin for our coordinate system we would like, we can set z=0 for the position of the load ZL. We will then divide the (top) Voltage Equation in [2] by the (lower) Current Equation in [2], and evaluate at z=0. We can set this equal to Equation [1], and we obtain Equation [3], since all of the complex exponential terms cancel out:
 [3] [3]
The ratio of the reflected voltage amplitude to that of the forward voltage amplitude is the voltage reflection coefficient. This can be solved for via the above equation:
 [4] [4]
The reflection coefficient is usually denoted by the symbol gamma, as in Equation [4]. Note that the magnitude of the reflection coefficient does not depend on the length of the line, only the load impedance and the impedance of the transmission line. Also, note that if ZL=Z0, then the line is perfectly "matched". In this case, there is no mismatch loss and all power is transferred to the load. At this point, you should begin to understand the importance of impedance matching: grossly mismatched impedances will lead to most of the power reflected away from the load (and the load is often an antenna, which is what we care about here). Note that the reflection coefficient can be a real or a complex number. A complex reflection coefficient indicates the current and voltage are out of phase, which will happen for loads that have an imaginary impedance, indicated they have some inductive or capacitive component.
Standing WavesWe'll now look at standing waves on the transmission line. Assuming the propagation constant is purely imaginary (lossless line), We can re-write the voltage and current waves as:
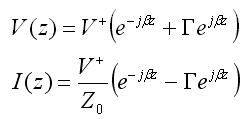
If we plot the voltage along the transmission line, we observe a series of peaks and minimums, which repeat a full cycle every half-wavelength. If gamma equals 0.5 (purely real), then the magnitude of the voltage would appear as:
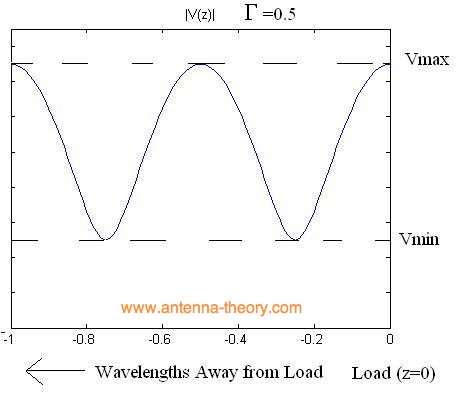
Similarly, if gamma equals zero (no mismatch loss) the magnitude of the voltage would appear as: 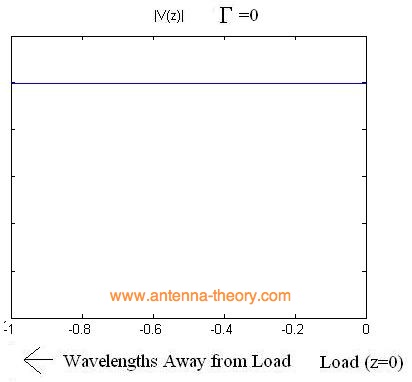
Finally, if gamma has a magnitude of 1 (this occurs, for instance, if the load is entirely reactive while the transmission line has a Z0 that is real), then the magnitude of the voltage would appear as:
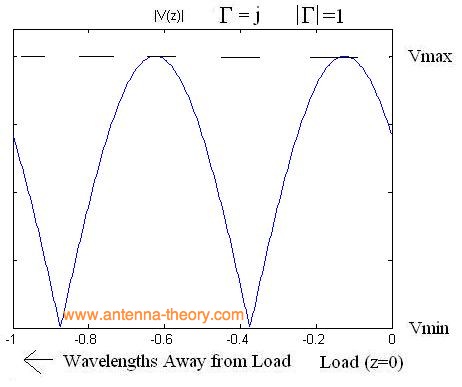
One thing that becomes obvious is that the ratio of Vmax to Vmin becomes larger as the reflection coefficient increases. That is, if the ratio of Vmax to Vmin is one, then there are no standing waves, and the impedance of the line is perfectly matched to the load. If the ratio of Vmax to Vmin is infinite, then the magnitude of the reflection coefficient is 1, so that all power is reflected. Hence, this ratio, known as the Voltage Standing Wave Ratio (VSWR) or standing wave ratio is a measure of how well matched a transmission line is to a load. It is defined as:
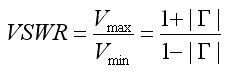
This parameter is commonly quoted in antenna spec sheets. It is typically given over a bandwidth, so that you have an idea of how much power is reflected by the antenna over a frequency range.
|
Previous: Tx Line Models and Z0