Envelope Correlation Coefficient (ECC)
|
A great way to improve wireless throughput (the amount of data you can send per second) is to move to a MIMO system (Multiple Input, Multiple Output). This means you have a radio capable of transitting and receiving multiple data streams simultaneously. And to do this, you need more than one antenna. Increased throughput is why your router at home has multiple antennas on it, and the reason that handheld devices (smartphones) are now using MIMO for both WIFI and LTE. This means smartphones are likely to have multiple WIFI and cellular antennas now. But how do we know we have a "good" antenna system design when we start including multiple antennas on a single product? It might occur to you that the antennas need to be somewhat independent in order to transmit simultaneous and independent data streams. And you'd be right. But what is independent? We mean that the antennas have good isolation, and that their radiation patterns are not the same, or at least not very "correlated". This leads us to define a "radiation pattern correlation metric", which the industry refers to as the Envelope Correlation Coefficient (ECC) Envelope Correlation Coefficient tells us how independent two antennas' radiation patterns are. So if one antenna was completely horizontally polarized, and the other was completely vertically polarized, the two antennas would have a correlation of zero. Similarly, if one antenna only radiated energy towards the sky, and the other only radiated energy towards the ground, these antennas would also have an ECC of 0. Hence, Envelope Correlation Coefficient takes into account the antennas' radiation pattern shape, polarization, and even the relative phase of the fields between the two antennas.
To get the mathematical formula for ECC, let's define the radiation pattern mathematically
as a vector function in
spherical coordinates.
We'll call the radiation pattern
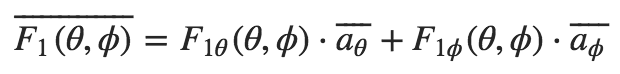 [1] [1]
In [1],
The envelope correlation coefficient is written mathematically in Equation [2]: 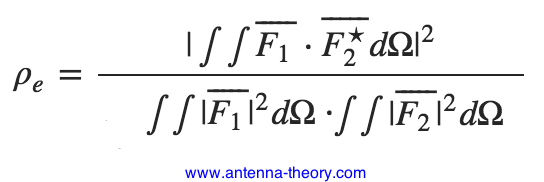 [2] [2]That's a lot of math. Rewritten in English, Equation [1] simply says the antenna's radiation pattern varies over a sphere (that is, it will vary in different directions from the antenna) and have an associated polarization (this is the vector part - the direction of the E-field). Equation [2] is a measure of how correlated two different antennas' radiation patterns are. If they are the exact same (so that F1=F2), the correlation coefficient would be 1.0. If they are completely independent, the correlation would be 0.
What's a good value for ECC? It turns out 0.5 is ok, higher than 0.5 is considered bad, and 0.3 or less is considered pretty good for MIMO applications. In general, correlation can be decreased via:
ECC and IsolationIt turns out that for highly efficient antennas (let's say >90% or > -1dB), the ECC can be completely determined from the antenna isolation (so you can just measure s12 and determine the ECC without measuring the antennas' radiation patterns. Why is this? Without going through the math, the reason is that if antennas produce the same (or highly correlated) radiation pattern, then they will also have tight coupling (or low isolation). This is because antennas have the same properties for transmit and receive (due to reciprocity), so if antenna 1 is transmitting a radiation pattern, antenna 2 will "see" this pattern and receive energy proportional to how correlated the antennas' radiation patterns are. It's a simple argument, but it turns out to be true. Hence, you can save a lot of time and focus on improving isolation in order to improve ECC. The formula for ECC in terms of isolation (s12) is given below:
 [3] [3]Equation [3] shows that the Envelope Correlation Coefficient can be measured with just a Vector Network Analyzer (VNA) and a 2-port S-parameter measurement. In the author's opinion, if you're developing a MIMO system, don't waste your time optimizing ECC. Optimize for isolation (s12), and you'll do just as well, with much simpler measurements. However, you'll need to know what ECC is, because it sounds really important, and people somewhat over-emphasize its importance in MIMO systems.
This page on Envelope Correlation Coefficient, or ECC, and its relation to antenna theory is copyrighted. Copyright antenna-theory.com, 2008-2016.
|
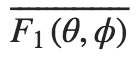 (the line on the top means it is a vector function),
and we can write the radiation
pattern as:
(the line on the top means it is a vector function),
and we can write the radiation
pattern as: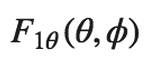 and
and
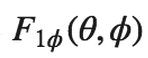 are complex functions;
the angle of the complex value represents the relative phase of the radiation pattern at each
point.
are complex functions;
the angle of the complex value represents the relative phase of the radiation pattern at each
point.