Spherical Coordinates
|
Understanding Spherical Coordinates is a must for the practicing antenna engineer. You are probably familiar
with Cartesian Coordinates - a position (point P) can be specified by a triplet like (x,y,z) where x is the distance
from the origin to the point along the X-axis, and so on (see Figure 1). Spherical coordinates use a different coordinate system,
one with spherical symmetry, which makes it very useful in engineering and physics in certain problems.
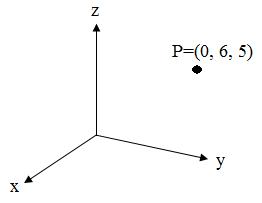 Figure 1. A point P defined in the Cartesian Coordinate System. The point P could be specified relative to the same origin in a different coordinate system. Spherical coordinates utilize three distinct coordinates: R - the magnitude of the distance between the origin and the point (always positive)
Any point specified in Cartesian coordinates as (x,y,z) can be re-expressed in spherical coordinates via the following transformation:
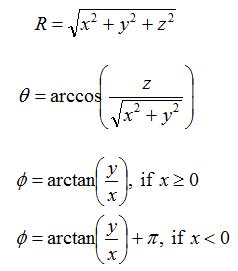 The above might look complicated, but after you've worked with it for a while it makes a lot of sense. The point P=(0,6,5) can be evaluated in spherical coordinates as:
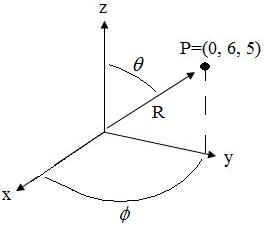
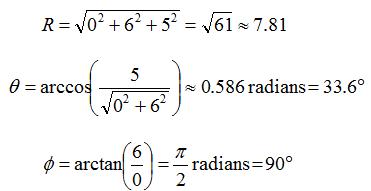 The coordinates are illustrated in Figure 2:
Spherical coordinates are popular for antennas, because we often are only interested in the antennas response in
a particular direction, not how far away something is (radiation patterns die off as 1/R^2 for all antennas in
the far field). In Cartesian coordinates, 3 variables need specified to determine the direction from the origin,
and it is not intuitive. For spherical coordinates, once it is understood, the polar angle
For practice, make sure the following table makes sense. I give a set of rectangular coordinates on the left, and the corresponding spherical coordinates on the right.
|
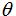- angle between the z-axis and the vector from the origin to the point (ranges from 0 to 180 degrees)
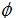- angle between the x-axis and the projection of the point onto the x-y plane (ranges from 0 to 360 degrees)