Frequency - More Advanced Concepts

Why is frequency so fundamental? To really understand that, we must introduce one of the coolest mathematical ideas ever (seriously), and that is 'Fourier Analysis'. I had a class on Fourier Analysis in grad school at Stanford University, and the professor referred to these concepts as 'one of the fundamental secrets of the universe'. Let's start with a question. What is the frequency of the following waveform? Figure 1. A simple waveform. 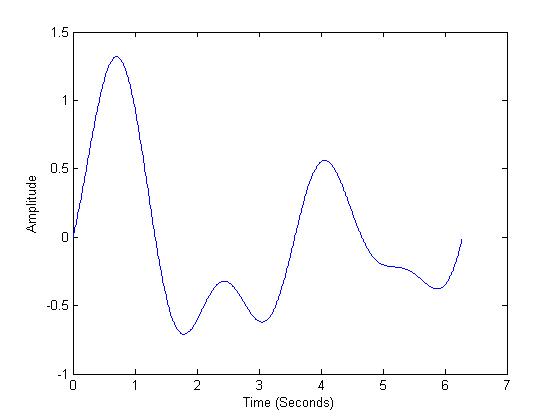Well, you'd look for what the period is and realize that it isn't periodic over the plotted region. Then you'd tell me the question was stupid. But here we go:

As an example, lets break down the waveform in Figure 1 into its 'building blocks' or the it's frequencies. This decomposition can be done with a Fourier transform (or Fourier series for periodic waveforms). The first component is a sinusoidal wave with period T=6.28 (2*pi) and amplitude 0.3, as shown in Figure 2.

Figure 2. First fundamental frequency (left) and original waveform (right) compared.

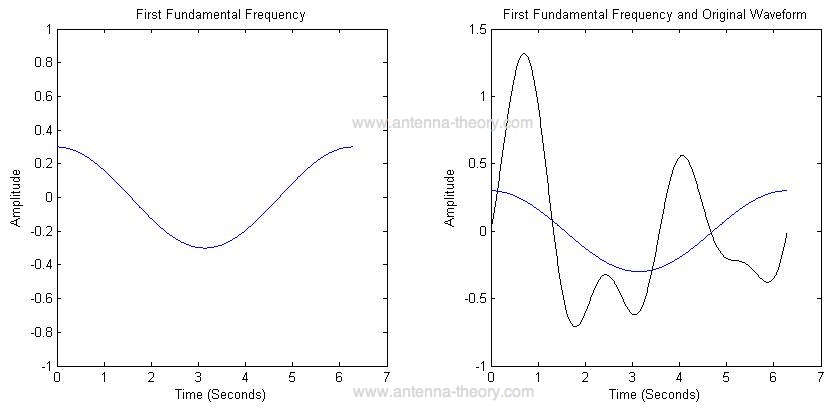
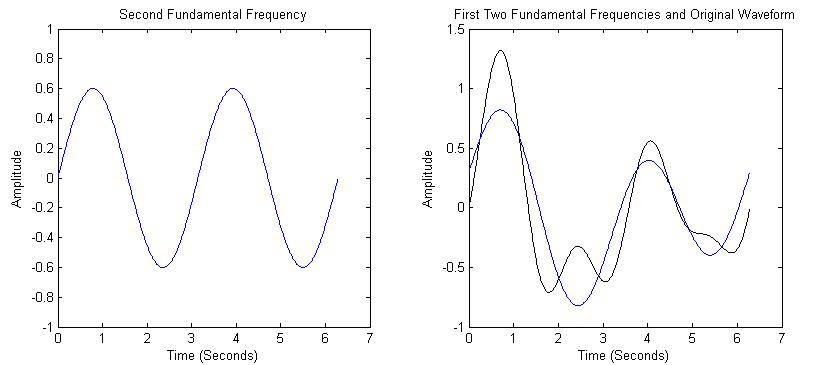
The second frequency will have a period half as long as the first (twice the frequency). The second component is shown on the left in Figure 3, along with the sum of the first two frequencies compared to the original waveform.

Figure 3. Second fundamental frequency (left) and original waveform compared with the first two frequency components.

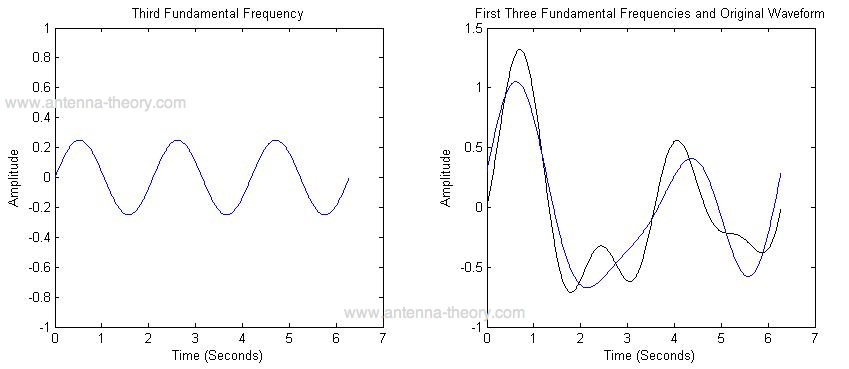
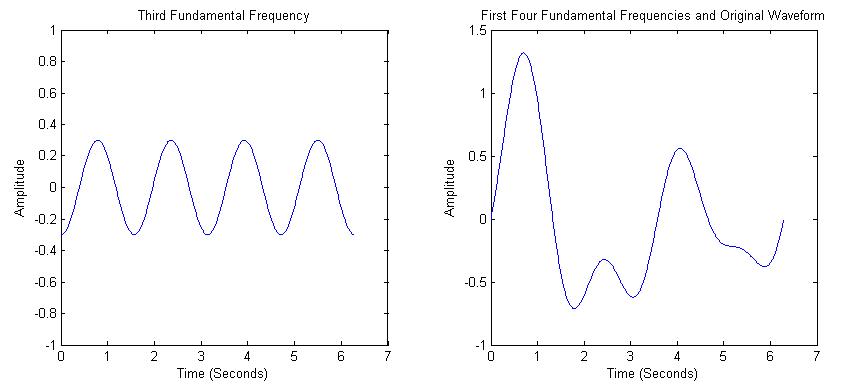
We see that the sum of the first two frequencies is starting to look like the original waveform. The third frequency component is 3 times the frequency as the first. The sum of the first 3 components are shown in Figure 4.

Figure 4. Third fundamental frequency (left) and original waveform compared with the first three frequency components.

Finally, adding in the fourth frequency component, we get the original waveform, shown in Figure 5.

Figure 5. Fourth fundamental frequency (left) and original waveform compared with the first four frequency components (overlapped).

While this seems made up, it is true for all waveforms. This goes for TV signals, cell phone signals, the sound waves that travel when you speak. In general, waveforms are not made up of a discrete number of frequencies, but rather a continuous range of frequencies. Hence, for all of antenna theory, we will frequency be discussing wavelength of frequency. Actual antennas radiate real world signals - data from the internet over WIFI, speech signals, etc etc etc. However, since every piece of information in the universe can be decomposed into sine and cosine components of varying frequencies, we always discuss antennas in terms of the wavelength it operates at or the frequency we are using. As a further consequence of this, the power an antenna can transmit is divided into frequency regions, or frequency bands. In the next section, we'll look at what we can say about these frequency bands.