Telescopes
|
On this page, we'll discuss the telescope from an antenna theory perspective. Telescopes aren't really antennas. Antennas are connected to a receiver or transmitter, and collect or transmit radiated electromagnetic waves. However, telescopes do collect electromagnetic waves - they just don't process them. Now, your eye does act as a receiver that processes the electromagnetic waves. When the telescope is placed up to the eye, it greatly increases the effective aperture of your eye, which means the peak antenna gain of your eye is significantly increased. The purpose of a telescope is to collect more of the extra light that your eye is missing:
 Figure 0. The Aperture of Your Eye is Small - So You Can't See Detail Far Away. The mission of the telescope is to collect light from a larger aperture and focus it towards your eye. The telescope and your eye are a lot like a Satellite Dish Antenna. Just as the satellite dish uses a large aperture (the dish) to collect incoming waves and reflect them to a single point (the receiving horn antenna), the telescope collects a lot of light (electromagnetic waves) and concentrates it to your eye. In this manner your eye has a much larger aperture than it normally would, and hence can "zoom in" on the night sky and view things it otherwise normally could not.
Side Note: For telescopes and optics, we draw straight lines to represent electromagnetic waves. This is an approximation,
and is only accurate for very high frequencies (very small wavelengths) or very large apertures. Hence, if you should not use
straight line ray optics to analyze a
half-wavelength dipole antenna.
Refracting TelescopesNow, have you ever stuck a stick into water and noticed that it appeared to bend? This is because light refracts (changes directions) in mediums with different refractive indices (or indexes). You can read all about that in the Electromagnetics Tutorial, as this basically follows directly from Maxwell's Equations. Basically, for non-magnetic materials (which is basically everything except iron alloys), light bends towards from the surface normal (that is, the direction perpendicular to the surface) in materials with higher dielectric constants. A material such as glass then can be used to bend light, which is an electromagnetic wave. Glass has a permittivity of about 4. So without going through more details now, a light ray would bend through a slab of glass as shown in Figure 1:
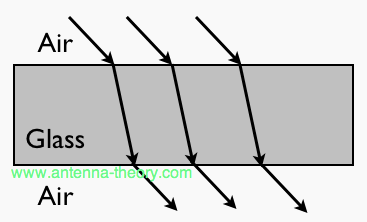 Figure 1. A Plane Electromagnetic Wave (Light) Being Refracted By Glass. Refracting telescopes use the above property to focus a large area of light towards your eye. Imagine we take a convex-shaped piece of glass, as shown in Figure 2. This piece of glass is made such that the light will leave it in a different direction than it entered, as shown in Figure 2:
 Figure 2. A Convex Lense Refracting Light. From Figure 2, we see that the convex shape of glass is very valuable. This can bend light in a direction that we choose, depending on how we shape the glass. In this manner, we can use this technique to collect a larger aperture of light than we get with our own naked eye. The principle of the refracting telescope uses two of these glass lenses, as shown in Figure 3:
 Figure 3. A Refracting Telescope. We need to define the focal lengths of the lenses in Figure 3. The focal length is how far from the lense parallel rays converge. Hence, the focal length of the big lense is f1, and the focal length of the smaller lense is f2, as shown in Figure 4:
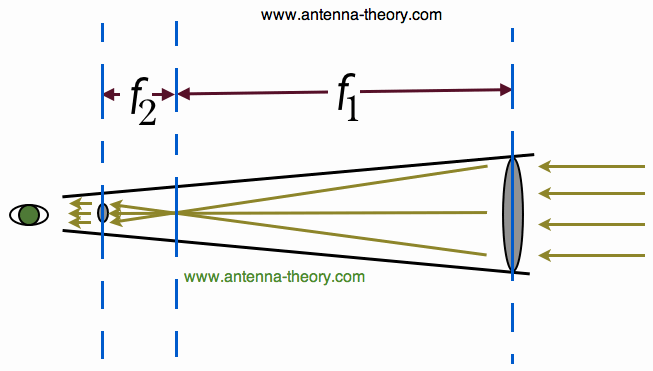 Figure 4. Focal Lengths. What kind of magnification can we get off of a refracting telescope as shown in Figure 3 and 4? We see that we have parallel rays coming into the telescope, and parallel rays leaving into the eye. So what is the net effect of the two lenses? Well - this is an antenna theory website so we are going to take a slightly different approach than normal. We are viewing the telescope/eye system as a receive antenna. But we know from antenna theory that (almost) all antennas satisfy reciprocity, which means they perform in the same manner whether they are receiving or transmitting. So instead of viewing the eye as a receiving sensor, let's suppose the eye is transmitting a figure as shown in Figure 5:
 Figure 5. Illustration of Telescope Magnification. Do you see what happened in Figure 5? The transmitted low rays (from the soldiers feet) get refracted by the first (smaller) lense and end up at the top of the larger lense, where they undergo refraction again and end up travelling in the same direction they started. The same thing happens for the rays near the soldiers head (which end up at the lower end of Figure 5). The result is the image is flipped and magnified. This is exactly what happens in a telescope. And from reciprocity, we know the antenna (telscope/eye system) works the same way whether transmitting or receiving. As a result, the telescope also magnifies when the eye acts as a receiver (i.e. when you are viewing the moon through your telescope). What is the resulting magnification for the telescope of Figure 5, with focal lengths f1 and f2? The first things we should note is that for a fixed f2, the larger f1 is, the more magnification we will have. In addition, for a fixed f1, the smaller that f2 is the more magnification we will have. If that's not clear, stare at Figure 5 and work through it so that it makes sense.
We can calculate the magnification (M) of a telescope as shown in Figure 6. We take two rays
(the red-orange rays) and note that the magnification is equal to the ratio of the input height (left side) to the output height (right side).
Now, using simple geometry, the angle between the two rays we can set to
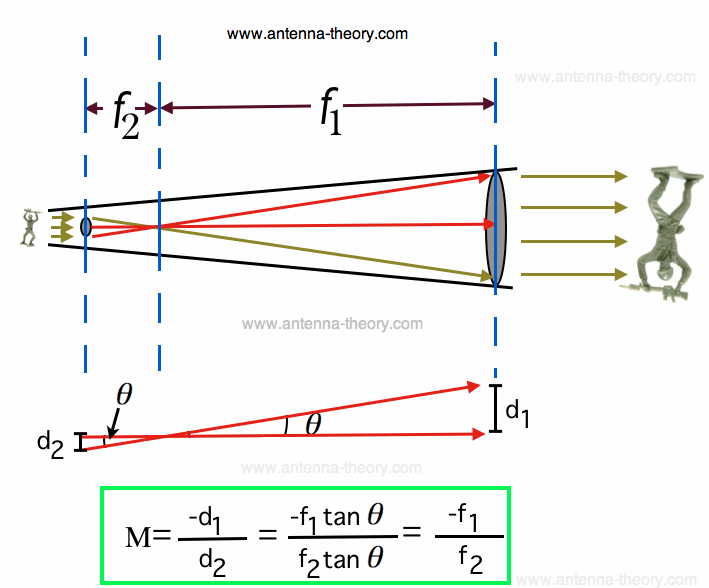 Figure 6. Here is the Derivation or Calculation for a Telescope's Magnification (M). Note that the magnification M is negative because the refracting telescope inverts the image. In addition, a couple things seem clear: As a result of the 2nd point, the magnification can be increased arbitrarily high by using a lense with a smaller focal distance. However, as the focal length of the smaller lense becomes smaller, you are still amplifying a fixed amount of light. As a result, while the magnification becomes larger the image becomes more dim. As a result, the maximum magnification of a telescope is limited by the size of the aperture (i.e. the size of the large lense that collects light). As a rule of thumb, the maximum magnification is proportional to the diameter of the aperture, given by Equation [1]:
Hence, if you have an 8" diameter telescope (203 mm), the maximum usable magnification is approximately M = 400. This is a general rule used by astronomers.
Antenna Theory (Home)
|
,
and a little geometry than shows that the magnification of a telescope is equal to the ratio of the focal lengths of the first (larger) lense
and the smaller (eyepiece lense):
