Slot Antennas
|
Slot antennas are used typically at frequencies between 300 MHz and 24 GHz. The slot antenna is popular
because they can be cut out of whatever surface they are to be mounted on, and have
radiation patterns that are
roughly omnidirectional (similar to a linear wire antenna, as we'll see). The polarization of the slot antenna is linear. The slot
size, shape and what is behind it (the cavity) offer design variables that can be used to tune performance. Consider an infinite conducting sheet, with a rectangular slot cut out of dimensions a and b, as shown in Figure 1. If we can excite some reasonable fields in the slot (often called the aperture), we have a slot antenna.
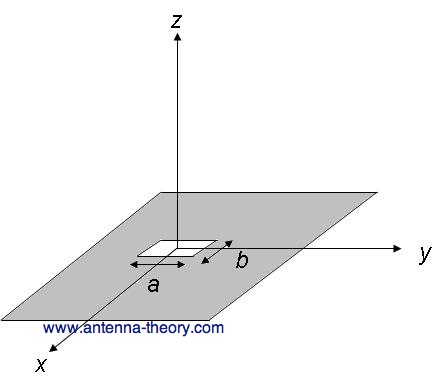 Figure 1. Rectangular Slot antenna with dimensions a and b. To gain an intuition about slot antennas, first we'll learn Babinet's principle (put into antenna terms by H. G. Booker in 1946). This principle relates the radiated fields and impedance of an aperture or slot antenna to that of the field of its dual antenna. The dual of a slot antenna would be if the conductive material and air were interchanged - that is, the slot antenna became a metal slab in space. An example of dual antennas is shown in Figure 2:
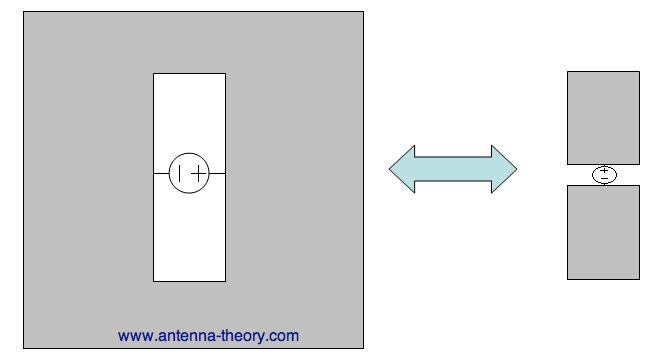 Figure 2. Dual antennas - (left) the slot antenna, (right) the dipole antenna. Note that a voltage source is applied across the short end of the slot antenna. This induces an E-field distribution within the slot, and currents that travel around the slot perimeter, both contributed to radiation. The dual antenna is similar to a dipole antenna. The voltage source is applied at the center of the dipole, so that the voltage source is rotated.
Babinet's principle relates these two antennas. The first result states that the
impedance of the slot antenna
(
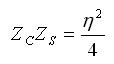
In the above,
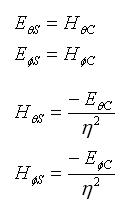 Hence, if we know the fields from one antenna we know the fields of the other antenna. Hence, since it is easy to visualize the fields from a dipole antenna, the fields and impedance from a slot antenna can become intuitive if Babinet's principle is understood. Note that the polarization of the two antennas are reversed. That is, since the dipole antenna on the right in Figure 2 is vertically polarized, the slot antenna on the left will be horizontally polarized.
Duality ExampleAs an example, consider a dipole similar to the one shown on the right in Figure 2. Suppose the length of the dipole is 14.4 centimeters and the width is 2 centimeters, and that the impedance at 1 GHz is 65+j15 Ohms. The fields from the dipole antenna are given by:
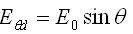 What are the fields from a slot at 1 GHz, with the same dimensions as the dipole?
Using Babinet's principle, the impedance can be easily found:
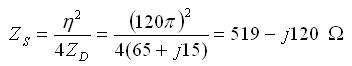 The impedance of the slot for this case is much larger, and while the dipole's impedance is inductive (positive imaginary part), the slot's impedance is capacitive (negative imaginary part). The E-fields for the slot can be easily found:
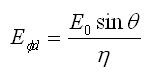 We see that the E-fields only contain a phi (azimuth) component; the slot antenna is therefore horizontally polarized.
Video: Analysis of the Slot AntennaTo see this material presented another way, here is a video on the analysis of the slot antenna. Some of the information below will be complimentary to the above analysis. Hence, if you enjoy short lectures this video may be of interest to you.
|
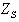 ) is related to the
impedance of its dual antenna (
) is related to the
impedance of its dual antenna (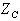 ) by the relation:
) by the relation: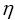 is the
is the