Scale Model Measurements
|
For the best estimate of an antenna's performance in real conditions, the measurement of the antenna should be performed in a location that closely resembles the antenna's real world operating environment. However, in some applications, precise measurements are desired, but real-world measurements aren't possible. For instance, suppose we are interested in an antenna's radiation pattern, antenna impedance, etc., and this antenna is to be operated on an airplane. Or suppose we are interested in the coupling between one antenna to another, both of which are operating on some random airplane. It is very expensive and difficult to mount the antennas on an airplane and then make the measurements (particularly the radiation pattern). In addition, often measurements are desired before the antenna locations are completely determined, so that we would like to try a few different positions to find an antenna that has a desired Field of View (FOV - the directions that are not obscured by the aircraft relative to the antenna) and a desired gain. One method we can use in this case is that of Scale Model Measurements. In this technique, a scaled model (typically a much smaller physical model of the actual structure) is used to represent the platform on which the antenna operates. Now the question is - is this valid? Can we get proper measurements from a smaller model? The answer is yes, if we know what we are doing. If you look at the page on frequency, I mentioned that frequency is one of the fundamental secrets of the universe - every signal can be represented as a combination of frequencies. Further, all of electromagnetics and antenna theory are completely described by Maxwell's Equations. If we are riding along a monochromatic (single frequency) electric field wave (stay with me here) and you encountered an obstacle, your behavior would only depend on the size of the obstacle in wavelengths. That is, plane waves respond the same wave to a perfectly conducting circular plate that is 3 wavelengths in diameter, no matter what the frequency. Hence, suppose we want to know the properties of a monopole antenna at f= 300 MHz (wavelength is 1 meter). Suppose this antenna is mounted on an airplane that is 30 meters long, so that the airplane is 30 wavelengths long. Suppose we build a scale model of our airplane that we can fit in our anechoic chamber, and this airplane model is 3 meters long. If we want to get the electromagnetic waves to behave the same way as they do on a real airplane at 300 MHz, we need to have the scale model be 30 wavelengths long. Hence, if we operate at f = 3000 MHz (3 GHz, where the wavelength is 0.1 meters), the model is now 30 wavelengths long. If we scale the monopole antenna by the same factor (10), then our measurements at 3 GHz on the scaled model will in theory be identical to measurements performed on the actual airplane at 300 MHz.
 Example of a Scaled Model Measurement of an Airplane. The quality of the results depends on the quality of the model. This method is a valid and often practiced method of antenna measurements in the aerospace and defense world. The following table is provided for understanding proper scaling. In the table, the model is assumed to be scaled down by a factor of n. For instance, in the previous paragraph, the airplane example had a scaled down model by a factor n=10. As another example, if n=100, then an L=100 meter real-world object would be represented by a scaled model that is L/n = 1 meter in size.
Table I is the result of working through the math in Maxwell's Equations. The good news is that some properties do not need scaled at all, particularly the permittivity and permeability (if you are modeling dielectrics or magnetic materials). In addition, the antenna impedance and gain do not need scaled either, which is a good thing. However, some things like conducitivity need to be increased by a factor of n in the scaled model. One way to understand this is to note that the resistance of the scaled model should be constant, and resistance is proportional to the conductivity of the object times the length divided by the cross sectional area. If the length goes down by a factor of n, and the cross sectional area goes down by a factor of n^2, then for constant resistance we require that the conductivity increases by a factor of n on the scaled model. Typically, the real world airplane has a shell that has high conductivity (metals). Hence, care needs exercised that the conductivity of the model is as high as possible. This can be done with polished high quality metals for the scaled model.
Antenna Measurements (Main)
|
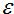 )
)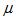 )
)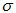 )
)