Folded Baluns

This balun is tricky to understand. Personally, I had to stare at it, then go to sleep, wake up, think about it some more, then it made sense. I will attempt to describe the operation here.

Note that the current on inner conductor of the coaxial cable contributes to the current that flows on the outer conductor. This could be cancelled by tying the inner conductor to the outside of the coaxial cable (because the current on the inner conductor is 180 degrees out of phase), which would cancel any net flow of current down the outer side of the coaxial cable. However, this would short-circuit any antenna connected to the coaxial cable, and thus we would have no radiation. The goal however, is to find a way to tie the current from the center cable of the coax to the outer shield such that the outer current is cancelled.

The folded balun is shown in Figure 1. The green line (which will be made of a cylindrical tube of the same dimensions and material as the main coax) is connected from the red dipole arm (that is connected to the center conductor) to the outside of the coaxial cable, a distance L from the end. If L is chosen to be a quarter-wavelength at the frequency of operation, then just as is the case for the bazooka balun, the impedance seen by this arm is infinite (due to the properties of transmission line theory and the quarter wavelength line). Hence, the first thing we need to note is that adding this balun does not affect the impedance of the dipole antenna - this means that if we can get the correct voltage to the antenna, it will radiate properly.

Figure 1. Folded Balun - the green line represents a cylinder of the same dimensions as the grey (main) coax.

Now, lets try to figure out why this will achieve balanced operation. Enlarging Figure 1 and showing all of the currents on the coaxial cable and balun (and getting rid of the other half of the dipole antenna because it does not need to be illustrated here), we have Figure 2. I've introduced another current, ID, which travels along the balun.

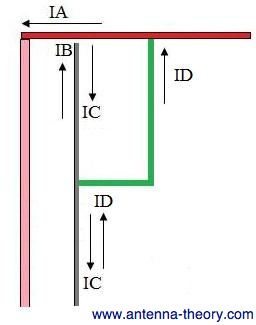Figure 2. Zoomed In on a Folded Balun with all Currents Shown.

We are going to have to understand all of the currents shown in Figure 2. The current IA is what travels down the center of the coaxial cable and onto the red arm of the dipole. The current IB is what flows on the inside of the outer shield of the coaxial cable and feeds the other dipole arm (not shown). The coaxial cable is a lossless transmission line - this means that the currents IA and IB are equal in magnitude but 180 degrees out of phase. That is, IA = - IB.

The current IC is what travels down the outside of the coaxial cable - this is the current that we would like to choke off. How large is IC? To determine this, we note that when the current IB travels to the end of the coaxial cable, it can either travel down the grey dipole arm (of Figure 1) or down the outside of the coaxial cable. The current IC will depend on what the impedance is looking down the outside of the coaxial cable relative to the impedance of the dipole arm. Lets call the impedance of the path on the outside of the coaxial cable as Zg.

The current ID must travel in the opposite direction to that of the current IC, because it is fed by the current IA, whereas IC is fed by IB. Here is the important observation. What is the magnitude of ID? The answer is - it must be equal to IC. Why? The answer lies in the following two observations:

First, note that the voltage on the inner conductor (pink line) is out of phase with the voltage on the outer conductor (grey line) - but they are of equal magnitude. Hence, if the attachment point of the balun to the red dipole arm (green to red connection in Figure 2), is made close to the center conductor, then the voltage at the balun connection point and the voltage at the connection between the outer conductor and the grey dipole arm are equal in magnitude but out of phase.

Second, at the point of attachment of the balun (the green-red connection in Figure 2), the impedance viewed down towards the outside of the coaxial cable must be equal to Zg. This is because the balun is made of the same shape and material as the main coaxial cable. Consequently, the impedance viewed down the balun and onto the main coax must be the same as that for the current IC.

Hence, if the voltages are equal in magnitude and out of phase, then the currents will cancel in the region below the balun. Consequently, balanced operation is restored.

This concept will probably take a few reads to make sense. Draw yourself some diagrams and work through it, and you will understand what is going on.

Note that because this balun requires a quarter-wavelength section to work properly, it is inherently narrowband. Away from the design frequency, the balun will no longer be a quarter-wave long and the properties described here will degrade.