Schelkunoff Polynomial Method
|
Instead of steering an antenna array (in which case we want to receive or transmit primarily in a particularly direction), suppose
instead we want to ensure that a minimum of energy goes in particular directions. The weights of an antenna array can be
selected such that the
radiation pattern
has nulls (0 energy transmitted or received) in particular directions. In this manner,
undesirable directions of interference, jamming signals, or noise can be reduced or completely eliminated. It turns out that this isn't real hard to do, either. In general, an N element array can place N-1 independent nulls in its radiation pattern. This just requires a little math to work through, and will be illustrated via an example. Let's assume we have an N element linear array with uniform spacing equal to a half-wavelength and lying on the z-axis. To start, the array factor of a uniformly spaced linear array with half-wavelength spacing can be rewritten using a variable substitution as:
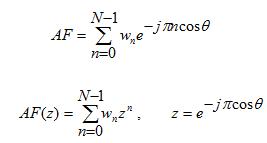 The above equation is simply a polynomial in the (complex) variable z. Recall that a polynomial of order N has N zeros (which may be complex). The polynomial for the AF above is of order N-1 zeros. If the zeros are numbered starting from zero, the zeros will be 0, 1, ..., N-2. The AF is rewritten then as:
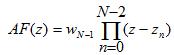
We've introduced variables,
To make the example concrete, let N=3. Suppose we want the array's radiation pattern to have
zeros at 45 and 120 degrees. We can simply use the equation for z above, and substitute
these values for the angle. We then obtain the corresponding zeros,
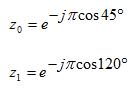
For simplicity, we'll let
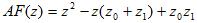 This AF must equal the original AF, so:
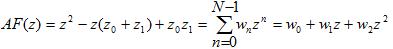 The weights then can be easily found to be:
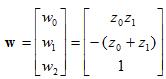
We already know what the
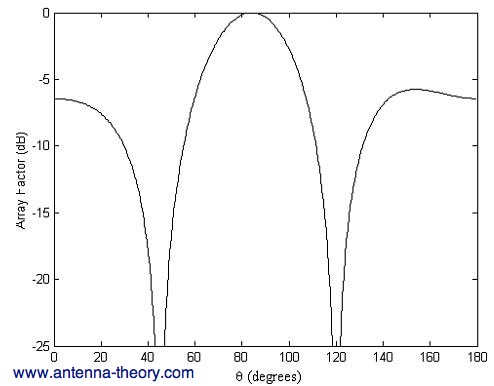 Figure 1. Magnitude of array factor. Observe that the radiation pattern has zeros at 45 and 120 degrees, exactly as we specified. This method can be used for whatever directions you want; however if N-1 nulls are selected for an N element array, the designer no longer has control over where the maximum of the radiation pattern is. This method can easily be performed on linear arrays with many more elements. This method can be The Schelkunoff Polynomial Method easily extends to planar and multi-dimensional arrays. The simplicity of placing nulls in the radiation pattern adds a powerful advantage for using arrays in practice. |
Antenna Arrays - Main
Antenna (Home)
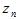 and have gotten rid of the weights. Hence, we can
choose the zeros
and have gotten rid of the weights. Hence, we can
choose the zeros 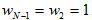 . The AF then becomes:
. The AF then becomes: