Minimum Mean-Square Error (MMSE) Weights (Part 4 - Example Useage)
|
In this section, we'll look at an example using MMSE weights, given by:
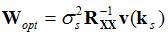
We'll consider an array with N=3 elements, with uniform half-wavelength spacing oriented
along the z-axis. We'll assume the desired signal is arriving from
Two cases will be considered. Case 1 will have a noise power given by
The required steering vector
corresponding to the desired wave vector
(
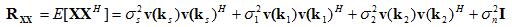 In the above, I is an NxN identitiy matrix. The weights can then be determined for both cases. The resulting normalized AFs are plotted in Figure 1.
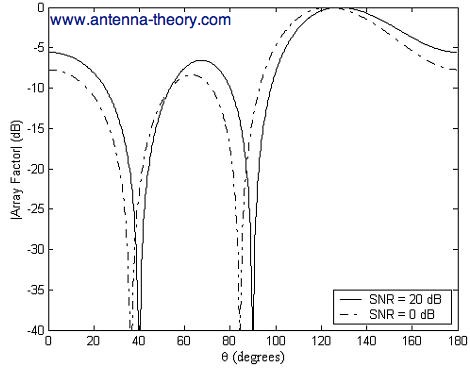 Figure 1. Normalized AFs for both cases using MMSE weights. The interferers are located at 40 and 90 degrees. The desired signal is located at 110 degrees. In both cases, the array tries to maximize power reception in the desired direction, and to minimize it near the interference locations. Note however that when the Signal-to-Noise Ratio (SNR) is high (implying low noise), as in Case 1 (SNR=20 dB), the array does a better job at placing nulls in the direction of the interference. In Case 2 (SNR=0 dB), when the noise is more dominant, the array places less of an emphasis on nulling out the interference, and the nulls are not exactly in the direction of the interference. The weights end up being more uniform in amplitude for the second case, which tends to increase the SNR for the array output. In this manner, the array is willing to sacrifice quality on blocking interference in order to minimize the noise affect. This result shows that the optimal weights vary as a function of the noise power.
|
Phased Arrays Home
Antennas (Home)
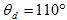 , with
a signal power given by
, with
a signal power given by 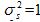 . Two interferers, arriving from
. Two interferers, arriving from
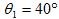 and
and 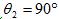 , each with interference power
given by
, each with interference power
given by 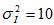 .
. 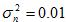 (SNR = 20 dB),
and Case 2 will have a noise power given by
(SNR = 20 dB),
and Case 2 will have a noise power given by 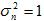 (SNR = 0 dB). The optimal
weights can be determined from the equation at the top of this page.
(SNR = 0 dB). The optimal
weights can be determined from the equation at the top of this page.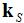 ) can be easily calculated by substituting in the definitions. Assuming the noise,
desired signal and interference are uncorrelated, the autocorrelation
matrix can be expanded and written as:
) can be easily calculated by substituting in the definitions. Assuming the noise,
desired signal and interference are uncorrelated, the autocorrelation
matrix can be expanded and written as: