Minimum Mean-Square Error (MMSE) Weights (Part 3)
|
On the previous page,
the MMSE weights were obtained as:
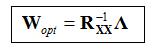
The above equation requires knowledge of the autocorrelation matrix and the vector
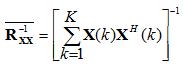
Assuming the desired signal is uncorrelated in time with the noise and interference (a reasonable assumption),
the vector
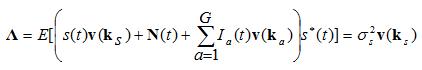
The above equation states the the vector
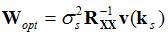 The optimal value of the Mean-Squared Error (MSE) can be evaluated using the formula for the mse and substituting in the optimal weights:
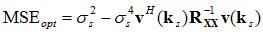 The fundamentals of this method have been presented. In the next section, we'll look at an example that illustrates the utility of this method.
|
Antenna Arrays Home
Antenna Home
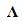 , both defined
, both defined 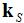 ) and the signal power
(
) and the signal power
(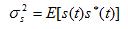 ) are known. These parameters can be estimated using a training sequence
to calibrate the array (training or known bits are often sent to calibrate a digital system to optimize
transmission). Using the above equation, the optimal weights can be rewritten as:
) are known. These parameters can be estimated using a training sequence
to calibrate the array (training or known bits are often sent to calibrate a digital system to optimize
transmission). Using the above equation, the optimal weights can be rewritten as: