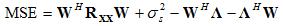Minimum Mean-Square Error (MMSE) Weights
|
We're deriving the optimal MMSE weights. Recall from the
previous page:
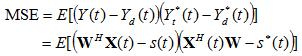 Multiplying the terms above, the MSE becomes
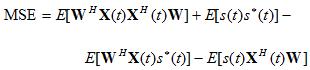 (1) (1)Because the weights are constant (don't vary with time), they can be pulled out of the expectation operator, and the first term in equation (1) simplifies to:
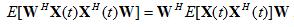
We'll now declare some definitions using equation (1).
We'll define a commonly used matrix in signal processing - the Autocorrelation Matrix, written
as
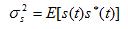 We'll define the correlation between the signals on the antennas and the desired signal as:
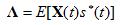 The third term can be written using the above definition as:
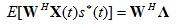 Finally, the fourth term in eq. (1) is the conjugate of the third term:
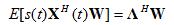 All these defintions are at first a bit cumbersome, but equation (1) can now be rewritten as:
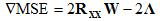 Setting this to zero and solving for W, the optimal MMSE-weights are:
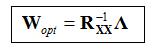 These are the optimal weights we have been looking for. The result is statistical - in terms of expected values of the desired signals. In the next section, we'll look at this in a little more depth and present an example that illustrates this weighting method.
|
Antenna Arrays Home
Antenna Home
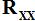 , which is defined to be:
, which is defined to be: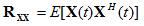
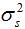 :
: