Thinned Antenna Arrays

One of the earliest methods of optimizing array geometry dates back to around 1960 and is known as "thinning arrays" or "array thinning". This method is relatively simple. A large uniformly spaced array (linear or planar) is used as a starting point. Large arrays are complex to build, have increased fabrication and setup costs, are heavier, etc; therefore, eliminating antenna elements from the array would be desirable, particularly if the array's performance is not significantly degraded. One method of achieving this goal is array thinning - systematically removing elements without a large degradation in performance. The elements can then be perturbed from their locations if necessary. To illustrate the utility of this method, a simple example will be presented. Consider a 20-element uniformly spaced linear array (with half-wavelength spacing), with positions given by: 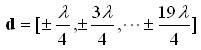To illustrate the concept of thinned arrays, lets remove some of the elements and perturb the locations a little, we have a 12 element linear array with positions given by: 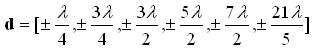Note that both arrays have approximately the same length. Assume that all the weights for the array are constant and set to one. The resulting Array Factors for both arrays are plotted in Figure 1. 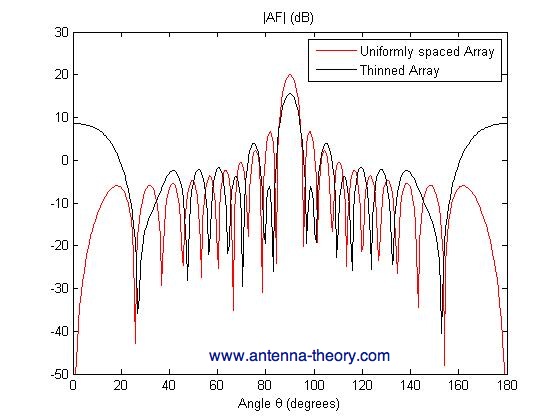Figure 1. Magnitude of Array Factor (dB) for Uniform 20-element array and thinned 12-element array. Some observations are immediattely apparent after observing Figure 1. First, the peak gain of the Array Factor decreased for the thinned array. This is because less elements make up the array; hence this result will always hold for thinned arrays. Second, the Sidelobe Level and beamwidth are approximately the same for the two cases, except for large angular separation from the main beam. Hence, the performance of the full uniform array can be approximately achieved using 40% fewer elements, which is often highly desirable. Side Note: The large sidelobes in the thinned array are easily eliminated. Recall that what is actually radiated by an antenna array is the product (pattern multiplication) of the Array Factor and the radiation pattern of the antennas that make up the array. Hence, by choosing an antenna that has low gain for small and large values of the polar angle theta (such as a simple dipole antenna, these sidelobes are instantly removed.

In previous example, I just removed some of the antenna elements and twiddled the spacing by hand to get something I liked. More general methods of array thinning are listed below. Thinning Based on an Empirical or Analytical Formula: Array thinning can be performed by using a set rule, which is advantageous because it requires no computation. For instance, array spacing can be designed to follow the prime number sequence, which leads to non-uniform and sparse spacing: 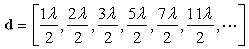Thinning based on space or density tapering: A successful method of lowering sidelobes in arrays is to decrease the magnitude of the weights away from the center of the array. This tapering is similar to "windowing" in digital signal processing. Having a uniform weight set across the array leads to higher sidelobes than when the weights taper down, in general. The density tapering approach uses uniform weights for all antennas; however, it removes antenna elements away from the center, in effect having less energy radiated away from the center of the array, which accomplishes the same effect as state above. Statistically thinned arrays: For very large arrays, a statistical method is often used for array tapering. In this approach, the probability for an element to lie in a particular position is proportional to the desired weighting for a weight-tapered array. For arrays with a large number of elements, this approach yields arrays that behave properly and have low sidelobes. Optimizing Algorithms: Finally, since computers are so computationally fast these days, thinning and placement optimization is often done via optimization algorithms. Examples include Genetic Algorithms (GA), the Particle Swarm Optimization (PSO) algorithm, and Simulated Annealing (SA). All of these methods employ some statistical optimization approach that guesses at the proper elements to remove, then removes them if this increases the performance of the array. This has been popular in the antenna literature over the past 15 years, primariliy because it is simple to implement and can achieve interesting results.