Hexagonal Sampling

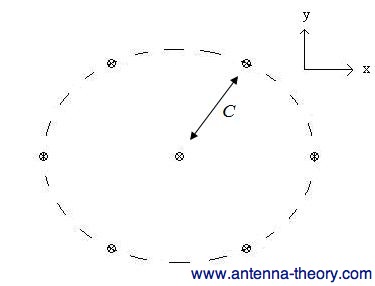Figure 1. Hexagonal Two-Dimensional Antenna Array.

The hexagonal structure is such that each element is a fixed distance (C in Figure 1) away from its 6 nearest neighbors. In addition, any 3 adjacent elements forms an equilateral triangle. This type of spacing is known as hexagonal because the outline of the outer 6 elements of the array in Figure 1 forms a hexagon; for arrays with more elements, the hexagons just repeat. Hence, the hexagonal array can have as many elements as desired.

Why this array? In multidimensional digital signal processing, it is known that sampling using the hexagonal lattice will produce the least aliasing for band-limited signals. In addition, the array has somewhat of a circular symmetry, so that the response towards distinct azimuth angles will not vary by a large degree.

In the author's experience, this array ends up being the optimal geometry for a large number of problems. For instance, for 2D arrays designed to have the minimum possible sidelobe level for a fixed beamwidth, the optimal geometry (associated with the optimal weights) will be a hexagonal array when N=7. In this case, the parameter C is chosen such that the beamwidth meets the specified criteria and grating lobes do not occur.

As a second example, an adaptive array developed by Raytheon that attempts to block out interference (or jamming signals) uses a hexagonal geometry. It turns out that by having a closely spaced sampling (small value of C in Figure 1), the nulls in the radiation pattern end up being wide, which help the array null out undesired directions.

I don't know of any other definitive reasons for choosing the hexagonal array; however I do know it is commonly employed. Slotted Waveguide Antennas are often arranged such that the slots have an approximately hexagonal spacing. In general, if you need to design the spacing for a 2D array, the hexagonal structure is a great place to start (and probably end up). In the next section, we'll look at optimizing array geometry.