The Short Dipole Antenna
|
The short dipole antenna is the simplest of all antennas. It is simply an open-circuited wire, fed at its center as shown in Figure 1.
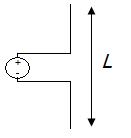 Figure 1. Short dipole antenna of length L. The words "short" or "small" in antenna engineering always imply "relative to a wavelength". So the absolute size of the above dipole antenna does not matter, only the size of the wire relative to the wavelength of the frequency of operation. Typically, a dipole is short if its length is less than a tenth of a wavelength:
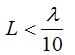
If the short dipole antenna is oriented along the z-axis with the center of the dipole at z=0, then the current distribution on a thin, short dipole is given by:
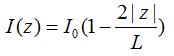
The current distribution is plotted in Figure 2. Note that this is the amplitude of the current distribution; it is oscillating in time sinusoidally at frequency f.
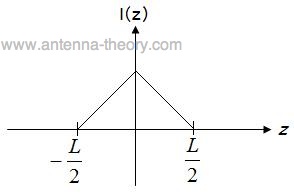 Figure 2. Current distribution along a short dipole antenna.
The fields radiated from the short dipole antenna in the far field are given by:
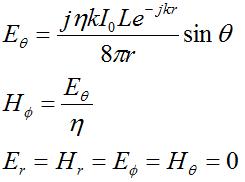
The above equations can be broken down and understood somewhat intuitively. First, note that
in the far-field, only the
This indicates that in the far-field region the fields are propagating like a plane-wave. Second, the fields die off as 1/r, which indicates the power falls of as 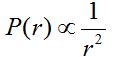
Third, the fields are proportional to L, indicated a longer dipole will radiate more power. This is
true as long as increasing the length does not cause the short dipole assumption to become invalid.
Also, the fields are proportional to the current amplitude
The exponential term:
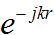 describes the phase-variation of the wave versus distance. The parameter k is known as the wavenumber. Note also that the fields are oscillating in time at a frequency f in addition to the above spatial variation.
Finally, the spatial variation of the fields as a function of direction from the antenna are given
by
In the next section further properties of the short dipole will be discussed.
Directivity, Impedance and other Properties of the Short Dipole Antenna
The directivity
of the center-fed short dipole antenna depends only on the
The polarization of this antenna is linear. When evaluated in the x-y plane, this antenna would be described as vertically polarized, because the E-field would be vertically oriented (along the z-axis).
We now turn to the input impedance of the short dipole, which depends on the radius a of the dipole. Recall that the impedance Z is made up of three components, the radiation resistance, the loss resistance, and the reactive (imaginary) component which represents stored energy in the fields:
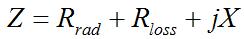 The radiation resistance can be calculated to be:
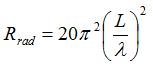
The resistance representing loss due to the finite-conductivity of the antenna is given by:
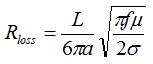 (Want to see where this comes from? See the Loss resistance derivation)
In the above equation
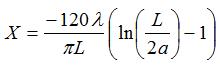
Note that the reactance is negative, indicating that the impedance is capacitive.
As an example, assume that the radius is 0.001
The radiation resistance is calculated to be 0.49 Ohms. The loss resistance is found to be 4.83 mOhms (milli-Ohms), which is approximatley negligible when compared to the radiation resistance. However, the reactance is -1695 Ohms, so that the input resistance is Z=0.49 - j1695. Hence, it would be very difficult to impedance match this antenna. Even if the reactance was cancelled out with a lossless inductor, very little power would be delivered from a 50 Ohm source to a 0.49 Ohm load.
For short dipole antennas that are smaller fractions of a wavelength, the radiation resistance becomes smaller than the loss resistance, and consequently this antenna can be very inefficient.
The bandwidth for short dipoles is difficult to define. The input impedance varies wildly with frequency because of the reactance component of the input impedance. Hence, these antennas are typically used in narrowband applications. In the next section, we'll look at general dipole antennas.
Antenna Theory (Home)
|
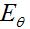 and
and
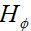 fields are nonzero. Further, these fields
are orthogonal and in-phase. Further, the fields are perpendicular to the
direction of propagation, which is always in the
fields are nonzero. Further, these fields
are orthogonal and in-phase. Further, the fields are perpendicular to the
direction of propagation, which is always in the
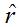 direction (away from the antenna). Also, the ratio of the E-field to
the H-field is given by
direction (away from the antenna). Also, the ratio of the E-field to
the H-field is given by
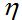 (the
(the 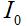 , which should make sense (more current, more power).
, which should make sense (more current, more power). 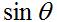 . For a vertical antenna oriented along the z-axis, the radiation
will be maximum in the x-y plane. Theoretically, there is no radiation
along the z-axis far from the antenna.
. For a vertical antenna oriented along the z-axis, the radiation
will be maximum in the x-y plane. Theoretically, there is no radiation
along the z-axis far from the antenna.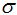 represents the conductivity of the dipole (usually very high, if made of
metal). The frequency f come into the above equation because of the
represents the conductivity of the dipole (usually very high, if made of
metal). The frequency f come into the above equation because of the
 and the length is 0.05
and the length is 0.05