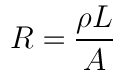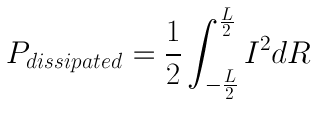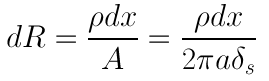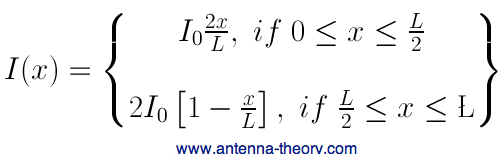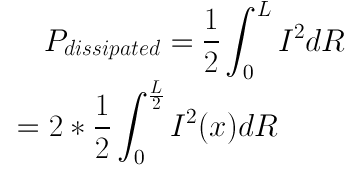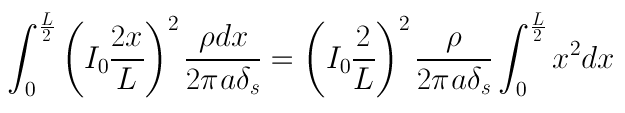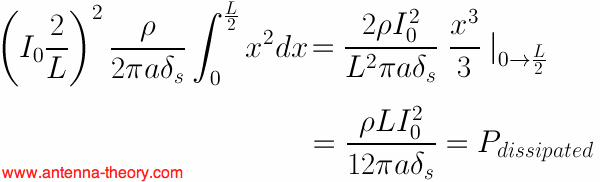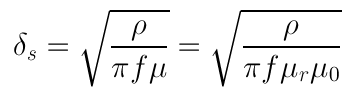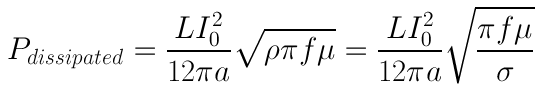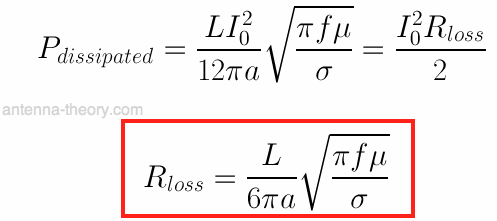The Short Dipole Antenna Loss Resistance
|
How do we derive the equation for the loss resistance of a short dipole antenna? We'll try to do that on this page.
Let's start with the equation for the d.c. (0 Hz) resistance (R) of a material with
resistivity (
The reason this equation is only valid at d.c. is because at higher frequencies, the current does not flow uniformly through the cross sectional area A. As a result, the loss resistance increases, because the current is actually flowing through a smaller area than the full cross section. This concept is known as skin depth, and is discussed on the skin depth page. If we want to calculate the power dissipated as a result of the finite-conductivity (or the resistivity) of a material with electric current flowing through it, then we can use equation [2]:
In equation [2], R is the total resistance, and I is the current that flows through the material. For the case of the short dipole antenna, we have a current that drops off linearly with distance:
 Figure 1. Current Distribution on a Short Dipole Antenna. To calculate the total power lost from this current, we use integration:
In the above equation, dR is the resistance of a small section of the antenna. We can approximate the current along a small section as constant, and so we can rewrite dR as:
In equation [4], we rewrote the cross sectional area as the skin depth times the circumference of the wire (2*pi*a). Does that make sense? If not, think about it for a while and prove it to yourself.
We can rewrite/shift the electric current distribution of I(x) into:
The reason Equation [5] was rewritten this way is in order to simply integrate the first section, and then multiply the result by 2. [We can avoid doing 2 integrals, because they will both produce the same value for loss.] The power dissipation equation then becomes:
We can substitute Equation [4] and I(x) to get:
Then we figure out the total dissipate power as:
Now we've gotten somewhere. If we substitute in the skin depth:
Euqation [8] then becomes:
If we set the power dissipated equal to an imaginary loss resistance (as if thisÊ was a simple ac circuit with a current flowing through of magnitude I0), we get:
Now, I'm missing a factor of a square root of 2 in there [sqrt(2)], and honestly I don't know where it comes from. ÊBut all the other terms are right, and you can see all the ideas behind how it is derived. Hopefully you understand why the loss increases with higher frequency (skin depth), why the loss is different than if we were measuring a block of material, and why the result is proportional to the square root of resistivity, instead of resistivity to the first power.
Antenna Theory (Home)
|
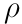), length L and cross sectional area A:
