The Parabolic Reflector Antenna (Satellite Dish) - 3
|
The fields across the aperture of the parabolic reflector is responsible for this antenna's radiation. The maximum possible
antenna gain
can be expressed in terms of the physical area of the aperture:
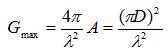
The actual gain is in terms of the
effective aperture, which is related to
the physical area by the efficiency term (
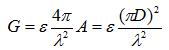 Understanding this efficiency will also aid in understanding the trade-offs involved in the design of a parabolic reflector. The antenna efficiency can be written as the product of a series of terms:
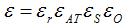 We'll walk through each of these terms.
Radiation Efficiency
The radiation efficiency
Aperture Taper Efficiency
The aperture radiation efficiency This efficiency can be improved by increasing the F/D ratio, which also lowers the cross-polarization of the radiated fields. However, as with all things in engineering, there is a tradeoff: increasing the F/D ratio reduces the spillover efficiency, discussed next.
Spillover Efficiency
The spillover efficiency
Other Efficiencies
There are many other efficiencies that I've lumped into the parameter
Calculating EfficiencyThe efficiency is a function of where the feed antenna is placed (in terms of F and D) and the feed antenna's radiation pattern. Instead of introducing complex formulas for some of these terms, we'll make use of some results by S. Silver back in 1949. He calculated the aperture efficiency for a class of radiation patterns given as:
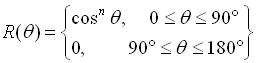
TYpically, the feed antenna (horn) will not have a pattern exactly like the above, but can be approximated well
using the function above for some value of n. Using the above pattern, the aperture efficiency of a
parabolic reflector can be calculated. This is displayed in Figure 1 for varying values of
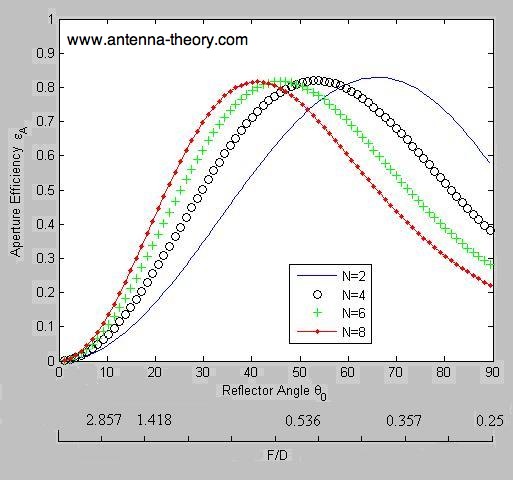
Figure 1. Aperture Efficiency of a Parabolic Reflector as a function of F/D or
the angle
Figure 1 gives a good idea on design of optimal parabolic reflectors. First, D is made as large as possible
so that the physical aperture is maximized. Then the F/D ratio that maximizes the aperture efficiency can be
found from the above graph. Note that the equation that relates the ratio of F/D to the angle
In the next section, we'll look at the radiation pattern of a parabolic antenna.
|
Antenna Theory (Home)
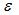 ).
This efficiency term will often be on the order of 0.6-0.7 for a well designed dish
antenna:
).
This efficiency term will often be on the order of 0.6-0.7 for a well designed dish
antenna: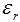 is the usual efficiency that deals with ohmic losses,
as discussed on the
is the usual efficiency that deals with ohmic losses,
as discussed on the
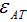 is a measure of how uniform the E-field is
across the antenna's aperture. In general, an antenna will have the maximum gain if the E-field
is uniform in amplitude and phase across the aperture (the far-field is roughly the Fourier Transform of
the aperture fields). However, the aperture fields will tend to diminish
away from the main axis of the reflector, which leads to lower gain, and this loss is captured within
this parameter.
is a measure of how uniform the E-field is
across the antenna's aperture. In general, an antenna will have the maximum gain if the E-field
is uniform in amplitude and phase across the aperture (the far-field is roughly the Fourier Transform of
the aperture fields). However, the aperture fields will tend to diminish
away from the main axis of the reflector, which leads to lower gain, and this loss is captured within
this parameter. 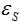 is simple to understand. This measures the amount of radiation from
the feed antenna that is reflected by the reflector. Due to the finite size of the reflector, some of the radiation
from the feed antenna will travel away from the main axis at an angle greater than
is simple to understand. This measures the amount of radiation from
the feed antenna that is reflected by the reflector. Due to the finite size of the reflector, some of the radiation
from the feed antenna will travel away from the main axis at an angle greater than 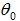 , thus
not being reflected. This efficiency can be improved by moving the feed closer to the reflector, or by increasing
the size of the reflector.
, thus
not being reflected. This efficiency can be improved by moving the feed closer to the reflector, or by increasing
the size of the reflector.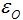 . This
is a major of all other "real-world effects" that degrades the antenna's gain and consists of effects such as:
. This
is a major of all other "real-world effects" that degrades the antenna's gain and consists of effects such as: